ბუნებრივი და ხელოვნური ფერდობების სეისმური მდგრადობის განსაზღვრა/ამოსაბეჭდი ვერსია
შინაარსი
- ბუნებრივი და ხელოვნური ფერდობების სტატიკური და სეისმური მდგრადობის ზოგიერთი ასპექტი
- მიწისძვრის შედეგად გრუნტის გათხევადების ეფექტის გავლენა ფერდობების სტატიკურ და სეისმურ მდგრადობაზე
- ფერდობების სტატიკური მდგრადობის განსაზღვრისათვის გამოყენებული საანგარიშო მეთოდები
- ზღვრული წონასწორობის მეთოდი
- ბლოკების ჩვეულებრივი მეთოდი
- ბიშოფის გამარტივებული მეთოდი
- სპენსერის მეთოდი
- ძალთა წონასწორობის მეთოდი მოდიფიცირებულ შვედურ მეთოდთან ერთად
- ჯანბუს ბლოკების განზოგადოებული მეთოდი
- მორგენშტერნისა და პრაისის მეთოდი
- სარმას მეთოდი
- სასრულო ელემენტის მეთოდი
- ზღვრული წონასწორობის მეთოდი
- ფერდობების სეისმური მდგრადობის განსაზღვრისათვის გამოყენებული საანგარიშო მეთოდები
- ფსევდო-სტატიკური (PS) მეთოდი
- პერმანენტული დეფორმაციის მეთოდი
- ნიუმარკის მეთოდი
- მაკდიზი-სიდის მეთოდი
- ფერდობების სეისმური მდგრადობის გაანგარიშება EN 1998-1:2004 და EN 1998-5:2004-ის მიხედვით
- საანგარიშო სეისმური ზემოქმედების განსაზღვრა
- გათხევადების ეფექტის გათვალისწინება ფერდობების სეისმური მდგრადობის გაანგარიშებისას
- ტოპოგრაფიული გაძლიერების ფაქტორი
- ფერდობების მდგრადობის გაზრდის ზოგიერთი ღონისძიება
- გრუნტის მათემატიკური მოდელების განვითარება და გამოყენება
დანართი. ქ. თბილისში „სატივეს“ მშენებარე ფერდობის სტატიკური და სეისმური მდგრადობის ანგარიში
გამოყენებული ლიტერატურაგამოყენებული ლიტერატურა
თავი 1 - ბუნებრივი და ხელოვნური ფერდობების სტატიკური და სეისმური მდგრადობის ზოგიერთი ასპექტი
ფერდობების მდგრადობის გაანგარიშების განვითარება გეოტექნიკაში მჭიდროდ არის დაკავშირებული გრუნტების მექანიკის განვითარებასთან და მასთან ერთად ერთ მთლიანობას შეადგენს.
ბუნებრივი ფერდობები, რომლებიც დიდი ხნის განმავლობაში ინარჩუნებენ მდგრადობას, ხშირად ინგრევიან გარემოს ტოპოგრაფიის შეცვლის, სეისმური ზემოქმედებისა და გრუნტის წყლების დინებისაგან გამოწვეული სიმტკიცის დაკარგვის და ძაბვების ცვლილების გამო. თუ ცნობილია, რომ ბუნებრივ ფერდობში არსებობს ძველი დაცურების ზედაპირი, რომელიც ხშირად წარმოადგენს შედეგს ადრე განვითარებული მეწყერისა ან ტექტონიკური აქტიურობისა, მაშინ ეს იძლევა საშუალებას ფერდობის ქცევის შეფასებისა მომავალში. ფერდობის მდგრადობის პრობლემა აქტუალური გახდა მას შემდეგ, რაც ადამიანის საქმიანობის შედეგად დაირღვა მყიფე ბალანსი ადამიანსა და ბუნებას შორის, რაც გამოიხატა ხელოვნური - ნათხარი და ნაყარი ფერდობების დაკონსტრუირების მოთხოვნილების გაზრდაში. ამ უკანასკნელმა კი თავისთავად დღის წესრიგში დააყენა ფერდობების საანგარიშო მეთოდებისა და კვლევების საშუალებების განვითარება, რის მიხედვითაც შესაძლებელი ხდება ფერდობების სტაბილურობის პრობლემების გადაწყვეტა. გეოლოგია, ჰიდროგეოლოგია და გრუნტის თვისებები წარმოადგენს ფერდობის მდგრადობის ცენტრალურ პრინციპულ საკითხებს და შესაბამისად ანგარიშები უნდა ეფუძნებოდეს ფერდობის ისეთ მოდელს, რომელიც ზუსტად ასახავს ფერდობის ზედაპირის პირობებს, გრუნტის ქცევას და ფერდობზე მოსულ დატვირთვას, რაც ასევე დაკავშირებულია ფერდობის წარმოშობასთან - ბუნებრივია ის თუ ხელოვნური.
სეისმური ზემოქმედების ეფექტის შესწავლა ერთერთი ცენტრალური საკითხია ფერდობების მდგრადობის განხილვისას.
მიწისძვრის დროს შესაძლებელია როგორც ბუნებრივი, ასევე ხელოვნური ფერდობების დანგრევა-დაზიანება, თუ მიწისძვრის მაგნიტუდამ 5,5-ს გადააჭარბა. ბუნებრივ ფერდობებზე შეიძლება ამ დროს განვითარდეს მეწყერი, რომელიც დასახლებულ პუნქტებს დიდი ნგრევით და მსხვერპლით დაემუქრება.
კატასტროფული მეწყერის მაგალითად მე-20 საუკუნეში გამოგვადგება 1920 წელს მიწისძვრით გამოწვეული მეწყერი ჩინეთში 100000-ანი მსხვერპლით; 1964 წლის მიწისძვრა ალიასკაზე, რომელსაც დიდი ნგრევა მოჰყვა; 1963 წელს იტალიაში ვაიონტის თაღოვანი კაშხალის აუზში განვითარებული მეწყერი, რომელმაც 2300 ადამიანი იმსხვერპლა /1/ და 2006 წელს თებერვალში ფილიპინებზე მომხდარი მეწყერი 2000 დაღუპულით.
გარდა ამისა მეწყერი აზიანებს ინფრასტრუქტურასაც, რაც დიდ მატერიალურ ზარალთან არის დაკავშირებული. ამას ადასტურებს ქვემოთ ფოტოებზე მოყვანილი შემთხვევები /13/
-
სურ. 1
-
სურ. 2
მეწყერით გამოწვეული მიწისქვეშა მილსადენის (სურ.1) და ჰიდრანტის (სურ.2) დაზიანება იაპონიაში.
მიწის ზედაპირის მიმართ დახრილი და ჩაუმაგრებელი ფერდობის გრუნტის ნაწილაკები სიმძიმისა და სხვა ძალების ზემოქმედებით ცდილობენ გადაადგილდნენ ქვემოთ ფერდის მიმართულებით, რომლის დროსაც სტატიკური წონასწორობა ფერდობისა შენარჩუნებულია მხოლოდ ან ხახუნის ძალის წინაღობით, ან შეჭიდულობის ან სხვა პასიური ძალებით. ეს წონასწორობა შეიძლება დარღვეული იქნეს, თუ მოხდა იმ ძალების დროებითი ზრდა, რომლებიც მოქმედებენ ფერდობის მიმართულებით ქვემოთ, ან თუ შემცირდება იმ გრუნტის ფენების წინაღობა ძვრისადმი, რომლებიც შეადგენენ ფერდობის სიზრქეს.
თუ მოხდა უეცარი დაცურება გრუნტის მნიშვნელოვანი მასისა ფერდობზე, მაშინ გვაქვს მეწყერი, რომელიც ორი ტიპისაა და განსხვავდება ერთმანეთისაგან გამოვლინების ფორმით. პირველი ტიპის შემთხვევაში დანგრევის პირველი ბზარები ჩნდება ფერდობის ზედა ნაწილში და შემდეგ დაძრული გრუნტის მასივი გადაადგილდება დაცურების ისეთ ზედაპირზე, რომელსაც დაახლოებით წრიული რკალის ფორმა აქვს და მას ცილინდრული დაცურების მეწყერი ჰქვია. მეორე ტიპის შემთხვევაში დაცურების ზედაპირად განიხილება გრუნტის მასივში არსებული რაღაც ბუნებრივად შესუსტებული ზონა, რომელიც ხშირად განლაგებულია ჰორიზონტალურ ან მასთან მიახლოებულ სიბრტყეში. ასეთ მეწყერს ჰქვია მეწყერი დაცურების სწორხაზოვანი უბნებით.
არსებობს კიდევ ნაკადის ტიპის მეწყერი, რომლის დროსაც მეწყერის ტანში გრუნტი გადადის ფარდობითად მყარიდან თითქმის გათხევადებულ მდგომარეობაში და შემდეგ იწყებს დენას ფერდობზე. ასეთ მეწყერს იწვევს ფხვიერ სტრუქტურიანი გაჯერებული ქვიშის ან წვიმით დასველებული ლიოსის გათხევადება მიწისძვრის დროს. ამ დროს გრუნტის მოცულობა მცირდება, იცვლება გრუნტის ნაწილაკებს შორის დაწნევა და ნეიტრალური დაწნევა გარე დატვირთვის მიხედვით. (ნეიტრალური დაწნევა ან ძაბვა არის წყლის დაწნევა ფორებში). ამას თან ერთვის გრუნტის დაჯდომა და ბზარების გაჩენა. გრუნტის მასივის შიგნით იზრდება ძვრის ძაბვები და მცირდება ძვრისადმი სიმტკიცე. მიწისძვრის დროს უმთავრესი მიზეზი ძვრისადმი სიმტკიცის შემცირებისა არის ფოროვანი დაწნევის სიჭარბე გაჯერებულ ფენებში, როცა არ ხდება ჭარბი ფოროვანი დაწნევის დისიპაცია ისე სწრაფად, როგორითაც იგი იზრდება შეჭიდულობის არამქონე გრუნტის ფენაში სითხის მაღალი შეღწევადობის უნარით და შედეგად იგი კარგავს ძვრისადმი სიმტკიცეს. ამ დროს მცირდება ეფექტური ძაბვები, რასაც შეუძლია გამოიწვიოს ფერდობის დანგრევა მიწისძვრის შეწყვეტის შემდეგაც (ძაბვები,რომლებიც იწვევენ გრუნტის მყარი ფაზის კუმშვას ან დეფორმაციას, არის ეფექტური ძაბვები).
გათხევადებული ქვიშის ფენებში დაწყებულ დაცურებაზე მიანიშნებს დაცურების ზედაპირის აშკარად ამოწევა. როგორც კი მიწისძვრით გამოწვეული გრუნტის მოძრაობა წყდება, დაცურების მოძრაობაც ჩერდება. თუ დაცურება ვითარდება დაბალი სიმტკიცის რბილ თიხაში, სიმტკიცის დაკარგვას თან სდევს დიდი გადაადგილება, რომელიც შეიძლება ისეთი დიდი იყოს, რომ მცურავმა მასებმა ვერ შეინარჩუნოს ხანგრძლივი არასტაბილურობა თვით მიწისძვრის შეწყვეტის შემდეგაც. გათხევადებული ქვიშის სტაბილურობის შენარჩუნება კი შესაძლებელია დრენაჟის სწრაფად გამოყენებით ან სტატიკური დატვირთვის მდგომარეობის აღდგენით, რაც მიწისძვრის შემდეგ ხდება.
დიდი მეწყერებისა და მთის მასივების დაცურების საწინააღმდეგოდ პრაქტიკული ღონისძიებების გატარება შეუძლებელია. იმისათვის, რომ მინიმუმამდე დავიყვანოთ მიწისძვრის დროს ფერდობების დანგრევის საშიშროება, აუცილებელია შესწავლილი იქნეს გრუნტების დინამიკური სიმტკიცე და წარმოქმნილი დინამიკური ძაბვები. არ შეიძლება გრუნტების სტატიკური მახასიათებლები ბრმად გადატანილი იქნეს დინამიკური მახასიათებლების შეფასებაზე, განსაკუთრებით წყლის არსებობის შემთხვევაში.
გრუნტის დაცურება ძირითადად ვითარდება ისეთი მიწისძვრების დროს, როცა მაგნიტუდა იცვლება 5,5-დან 8,8-მდე და ეპიცენტრული მანძილი _ რამდენიმე კმ-დან ასეულ კმ-მდე. (ეს საკითხი განსაკუთრებით აქტუალურია საქართველოსთვის, რომლის მთელი ტერიტორიის სეისმურობა 7_9 ბალით განისაზღვრება. ეს კი იმას ნიშნავს, რომ შესაძლო მიწისძვრის გამოვლინების ინტენსიურობა რიხტერის სკალით 6-7 იქნება. მაგ. 1991 წლის რაჭის მიწისძვრის მაგნიტუდამ 6,9-ს მიაღწია. ჩვენ ტერიტორიაზე გვაქვს ჟინვალის მიწის კაშხალი, რომლის ფერდობების სეისმურ მდგრადობაზე ბევრი რამეა დამოკიდებული და მათ შორის თბილისის წყალმომარაგებაც. თვით თბილისში აქტიურად მიმდინარეობს მაღლივი მშენებლობები, რომლებიც ხშირ შემთხვევაში ფერდობების ათვისებით ხდება. ამიტომ საჭიროა განისაზღვროს ასეთი ფერდობების სეისმური მდგრადობა და პროგნოზიც კი, რაც გულისხმობს მეწყერის წარმოშობის შესაძლებლობის პროგნოზირებას განხილულ ფერდობზე შემდგომში ბუნებრივი პირობების შეცვლასა და სეისმური ზემოქმედების შემთხვევაში, ან მეწყერის განვითარების ხარისხის პროგნოზირებას იქ, სადაც ცნობილია საინჟინრო-გეოლოგიური პირობები, მაგრამ არასოდეს არ ჩატარებულა მეწყერის წარმოშობის პირობების შესწავლა.)
ფერდობის არასტაბილურობა დაკავშირებულია გრუნტების სიმტკიცის შემცირებასთან, რასაც თან სდევს მათი ჩამონგრევა იქ, სადაც სუსტი გრუნტები განფენილია სუსტი შეჭიდულობის მქონე ზედაპირული გრუნტების ქვეშ. როგორც კი ქვედა ფენები კარგავენ ამტანუნარიანობას მიწისძვრის დროს ზედაპირული ფენების დიდი მასები იწყებენ მოძრაობას. მთის ქანების მოწყვეტა ხშირად ხდება დამრეცი ფერდობების შემთხვევაში ან ტექტონიკურ ნაპრალთან ახლოს. პირველი ბზარები კი ჩნდება ფერდობის ზედა ნაწილში.
მიწისძვრის შემთხვევაში ფერდობზე მეწყერის განვითარების შესაძლებლობა დამოკიდებულია ისეთ ფაქტორებზე, რომლებიც შეიცავენ მონაცემებს ფერდობის გეომეტრიაზე, გეოლოგიაზე, ფერდობის ფუძის სეისმოლოგიურ მახასიათებლებზე, გრუნტის წყლის რეჟიმზე, წინასწარ არსებულ ჩამონახეთქების ზონაზე, ამინდზე და სხვა.
ფერდობები ხდება სტატიკურად არასტაბილური, როდესაც ძვრის ძაბვები პოტენციალურ ნგრევის ზედაპირზე აჭარბებს გრუნტის ძვრისადმი მედეგობას და ამას როდესაც ემატება მიწისძვრით გამოწვეული ძაბვები, იწყება ნგრევა. ასე რომ ფერდობის სეისმური სტაბილურობა დამოკიდებულია მის სტატიკურ სტაბილურობაზე.
ფერდობების სტატიკური მდგრადობის ანგარიში ნიშნავს გრუნტის იმ მასების სტაბილურობას, რომლებიც შემოფარგლულია პოტენციალურად დაცურების ზედაპირით ქვემოდან და თვით ფერდობის ზედაპირით ზემოდან. ის ძალები და მომენტები, რომლებიც იწვევენ გრუნტის მასების არასტაბილურობას, შედარებული უნდა იქნეს იმ ძალებთან და მომენტებთან, რომლებიც შეინარჩუნებენ ფერდობის სტატიკურ მდგრადობას.
ფერდობის სტატიკური მდგრადობის განსაზღვრისათვის გამოიყენება მეთოდები, რომლებიც ცნობილია როგორც ზღვრული წონასწორობის და რომელთა ძირითადი იდეა მდგომარეობს ჩამონგრევის ზედაპირის მოხაზულობის განსაზღვრაში და ამ ზედაპირის გასწვრივ ძაბვების სიდიდეების გამოთვლაში, რაც ნიშნავს დაცურების ზედაპირის შიგნით მოთავსებული გრუნტის მასივისა და გრუნტის თავისუფალი ზედაპირის სტატიკურ წონასწორობის მდგომარეობაში ყოფნას. ფერდობის მდგრადობის ხარისხის განმსაზღვრელად მიღებულია მდგრადობის მარაგის კოეფიციენტი, ანუ უსაფრთხოების ფაქტორი,F. ფართო გაგებით ეს უკანასკნელი შეიძლება განიმარტოს როგორც სიდიდე პოტენციალური წინაღობის ძალების ფარდობისა იმ აქტიურ ძალებთან, რომლებსაც შეუძლიათ გამოიწვიონ გრუნტის დაცურება. ფერდობი, რომელიც იმყოფება ზღვრულ წონასწორობაში, ხასიათდება 1-ზე მეტი სიდიდის უსაფრთხოების ფაქტორით. ჩვეულებრივად საანგარიშო უსაფრთხოების ფაქტორი იცვლება 1÷1,5.
უსაფრთხოების ფაქტორის გამოთვლა უმეტესად ტარდება 2 განზომილებიანი განივი კვეთისა და ბრტყელი დეფორმაციის მდგომარეობისათვის. თუ უსაფრთხოების ფაქტორის გამოთვლა ხდება 3 განზომილებიანი მოდელით, მაშინ მისი მნიშვნელობა იქნება უფრო მეტი, ვიდრე 2 განზომილებიანი მოდელით გაანგარიშებისას. ეს სამართლიანია ყველა ნათხარი და ნაყარი ფერდობებისათვის,მაგრამ არა მეწყერის შემთხვევაში /30/. 2 განზომილებიანი მოდელით ანგარიშის პრინციპები ზოგიერთი დამახასიათებელი გრუნტებისათვის შემდეგნაირად არის ჩამოყალიბებული: 1. გრუნტები არასაკმარისი ბმულობით, რომელთაც გააჩნიათ მხოლოდ წინაღობა ძვრისადმი, ვერ გაუძლებენ დატვირთვას, თუ ფერდობის დახრის კუთხე ნაკლებია გრუნტის შიდა ხახუნის კუთხეზე. 2. გრუნტები, რომელთაც გააჩნიათ მხოლოდ შეჭიდულობა: ასეთ შემთხვევაში დაცურების წრიული ზედაპირის გასწვრივ ნაპოვნი მაქსიმალური ძაბვა ნაკლები უნდა იყოს გრუნტის დაცურების ხვედრით წინაღობაზე და ფერდობი მდგრადია; 3. გრუნტები, რომელთაც გააჩნიათ წინაღობა ძვრისადმი და შეჭიდულობა: თუ გრუნტის წინაღობის ძალა თავსებადია გრუნტის სიმტიცესთან, ფერდობის მდგრადობა უზრუნველყოფილია /1/. პოტენციალური დაცურების ზედაპირის შერჩევა ხდება მანამდე, სანამ ყველაზე კრიტიკული ზედაპირი (უსაფრთხოების ფაქტორის უმცირესი სიდიდე) არ მოიძებნება. ფერდობების სტატიკური მდგრადობის ანგარიშისათვის დაცურების ზედაპირის შედგენა ხდება ხაზებისა და რკალების ისეთი კომბინაციისათვის, რომელიც იძლევა უსაფრთხოების ფაქტორის მინიმალურ სიდიდეს. ანგარიშში უნდა განიხილებოდეს ფერდობის სრული სიმაღლე. დაცურების ზედაპირის ტიპების მაგალითები მოყვანილია ნახ. /33/. გვხვდება დაცურების ზედაპირის შემდეგი ტიპები:
- წრიული დაცურების ზედაპირი _ გამოიყენება ისეთი ფერდობების გაანგარიშებისათვის, რომლებშიც გვხვდება ჰორიზონტალური დამჭერი ქანების დაფენება ან რომლებიც შედგენილია შედარებით ჰომოგენური გრუნტისაგან (ნაყარი ფერდობები.ნახ. 1,ა-ბ).
- დაცურების ზედაპირი წარმოადგენს ისეთი ხაზების კომბინაციას, რომელიც გამოიყენება ჰომოგენური და რბილი გრუნტით აგებული ფერდობების, ზოგჯერ გეოლოგიური რღვევებით, გაანგარიშებისათვის (ნახ. 1,ც)
- გვხვდება გაუმაგრებელი ქანების დაფენების სიბრტყის გასწვრივ პოტენციალური ნგრევა, რაც გაანგარიშებული უნდა იყოს (ნახ.1, დ)
- კომბინირებული დაცურების ზედაპირი, რომელიც შედგება წრფივი დაცურების ზედაპირისაგან ქანების დაფენების სიბრტყის გასწვრივ ფერდობის ზედა ნაწილში და დაცურების ზედაპირისაგან ქანების დაფენების განივად ფერდობის ქვედა ნაწილში, გამოყენებული უნდა იქნეს იქ, სადაც ქანების დაფენების სიბრტყე დახრილია. ამ შემთხვევაში საჭირო გახდება დაცურების ზედაპირის იმ ნაწილის ორიენტაციის ცვლა, რომელიც კვეთავს ფენების საზღვრებს, რათა შეიქმნას კინემატიკურად მისაღები ხაზის გეომეტრია (ნახ.1, ე).
ნახ. 1, a - b. წრიული დაცურების ზედაპირის გამოყენების მაგალითები
ნახ. 1, c. არსებული მეწყერის შემთხვევაში სპეციფიური დაცურების ზედაპირის გეომეტრიის გამოყენების მაგალითი
ნახ. 1, d. დღის სინათლეზე გამოსული ქანების დაფენების სიბრტყიანი ფერდობის პოტენციალური კრიტიკული დაცურების ზედაპირი
ნახ. 1, e. ქანების დაფენების გასწვრივ და განივად წარმოქმნილი დაცურების ზედაპირი (კანიონში ნაყარი გრუნტი ან ალუვიუმი)
ნახ. 1, f. ქანების დაფენების გასწვრივ და განივად წარმოქმნილი დაცურების ზედაპირი - კონტრფორსიანი შევსებით
თუ ძვრის მედეგობა გრუნტისა დაცურების ზედაპირის გასწვრივ აჭარბებს წონასწორობის შესანარჩუნებლად საჭირო მედეგობას, მაშინ გრუნტის მასები არასტაბილურია. სტაბილურობა და არასტაბილურობა გრუნტის მასებისა დამოკიდებულია მათ წონაზე, გარეგან ძალებზე, რომლებიც მათზე მოქმედებენ, ძვრისადმი სიმტკიცეზე, წყლის ფოროვან დაწნევაზე დაცურების ზედაპირის გასწვრივ და სხვა.
ზღვრული წონასწორობის მეთოდს იყენებენ უკვე მრავალი წელიწადია ბუნებრივი და ხელოვნური ფერდობების ანგარიშისათვის. ამ მეთოდით ძალა ან მომენტი აწონასწორებს გრუნტის მასას განხილული ჩამონგრევის ზედაპირის ზემოთ. გრუნტი ამ ზედაპირზე განიხილება როგორც სრულიად არადეფორმირებადი ტანი და მისი ძვრისადმი სიმტკიცე თანაბარია ჩამონგრევის ზედაპირის გასწვრივ ყველა წერტილში. ამ შემთხვევაში უსაფრთხოების ფაქტორი მუდმივია მთლიანად ჩამონგრევის ზედაპირის გასწვრივ. ეს არის დაშვება, რადგან რეალურად ეს უკანასკნელი მუდმივი არ არის.
ზღვრული წონასწორობის მეთოდები სხვადასხვაგვარია და მათში უსაფრთხოების ფაქტორი იანგარიშება სტატიკური წონასწორობის ერთი ან მეტი განტოლების გამოყენებით. უმეტესი ზღვრული წონასწორობის მეთოდებისა, როგორიცაა: ჩვეულებრივი მეთოდი ბლოკებისათვის (ფელენიუსის), ბიშოფის გამარტივებული მეთოდი, მოდიფიცირებული შვედური მეთოდი, სპენსერის მეთოდი, ჯანბუს ბლოკების განზოგადოებული მეთოდი, მორგენშტერნისა და პრაისის მეთოდი საზღვრავენ ფერდობის სტატიკურ წონასწორობას გრუნტის მასების დაყოფით, რომლებიც განთავსებულია დაცურების ზედაპირის ზემოთ, ვერტიკალური ბლოკების სასრულო რიცხვის სახით /3,4/
ზღვრული წონასწორობის მეთოდებში მიღებული დაშვება მდგომარეობს შემდეგში: იგულისხმება, რომ უსაფრთხოების ფაქტორი მუდმივია დაცურების ზედაპირის გასწვრივ, თუმცა, როგორც უკვე ავღნიშნეთ ზემოთ, ფაქტიურად ეს ასე არ არის. ყველა ეს მეთოდი თხოულობს პოტენციალური დაცურების ზედაპირის განსაზღვრას უსაფრთხოების ფაქტორის მიხედვით. ამ მოხაზულობის შერჩევა გრძელდება მანამდე, ვიდრე არ განისაზღვრება ამ უკანასკნელის მინიმალური სიდიდე. ანგარიშის გამარტივებისათვის დაცურების ზედაპირს განსაზღვრავენ როგორც წრიულს ან შედგენილს მცირე სწორი ხაზებისაგან. წრიული დაცურების ზედაპირი (ნახ.2) ხშირად გამოიყენება ანგარიშის დროს, რადგანაც ის მოსახერხებელია წრის ცენტრის მიმართ მომენტების შეჯამებისათვის, ამავე დროს წრის გამოყენება ამარტივებს ანგარიშებს. ამიტომ წრიული დაცურების ზედაპირი გამოიყენება ანგარიშის დაწყებიდან თითქმის ყოველთვის ძირითადად ჰომოგენური ფერდობებისათვის.
ნახ.2. წრიული დაცურების ზედაპირი.
კრიტიკული დაცურების ზედაპირი განსაზღვრულია როგორც ზედაპირი ყველაზე დაბალი უსაფრთხოების ფაქტორით.
სასრულო ელემენტის მეთოდის გამოყენება ფერდობების მდგრადობის ანგარიშისას შეიძლება გადაადგილებისა და ძაბვების გამისათვლელად, რომელსაც იწვევს მოდებული დატვირთვა. ამ მეთოდით შესაძლებელია გადაადგილების განსაზღვრა რთული დანგრევის მექანიზმის პირობებშიც, როდესაც ჩართულია ფერდობის გამაძლიერებელი სტრუქტურული ელემენტები, როგორიცაა: გეოტექსტილი, ბეტონის საყრდენი კედლები ან ხიმინჯები.
ხელოვნური ფერდობების მდგრადობისათვის დიდი მნიშვნელობა ენიჭება კაშხალის ან დამბის ფერდობზე შუასადების სისტემის დაპროექტებას, რომელიც შედგება ერთი ან მეტი გრუნტისა და/ან გეოსინთეტური მასალის ფენისაგან, როგორიცაა გეომემბრანა, გეოსინთეტური თიხის შუასადები, გეონეტი ან გეოტექსტილი. ამ შუასადებებს შორის ან მათ ზემოთ არის მოწყობილი სადრენაჟო ფენები. თუ ფერდის დაცურება ხდება გეომემბრანის ქვემოთ კომპაქტურად დატკეპნილ თიხის შუასადებსა და გეომემბრანის ზედაპირს შორის, გეომემბრანა შეიძლება გაიჭიმოს და გასკდეს ფერდობის სტატიკური და მით უმეტეს სეისმური დატვირთვის შემთხვევაში. გეომემბრანის გახეთქვამ თავის მხრივ შეიძლება გამოიწვიოს ფერდობის ფუძის გაგლეჯვა. ფერდობში შიდა დაზიანება ვითარდება ისეთ შემთხვევაში, როცა შუასადების სისტემის ერთი გეოსინთეტური ფენა ცურავს მეორე გეოსინთეტურ ფენაზე. სრიალი ასეთ შემთხვევაში შესაძლებელია, თუ ძვრისადმი მედეგობა ზედაპირებს შორის გაცილებით მცირეა, ვიდრე ის ძვრის ძალები, რომლებიც ზედაპირის ზემოთ მასალაში წარმოიქმნება. თუ ძვრის ძალები მეტია, ვიდრე ხახუნის ძალები ზედაპირებს შორის, მაშინ განვითარდება სრიალი, რასაც შედეგად მოჰყვება რღვევა გეოსინთეტიკაში და შედეგად ფერდობის დანგრევა. ამიტომ ფერდობის მდგრადობის ანგარიშისას გათვალისწინებული უნდა იყოს გრუნტისა და გეოსინთეტური მასალის ძვრისადმი მედეგობა /10/. გეოსინთეტური დაფარვის შემთხვევაში გადაადგილების განსაზღვრის მნიშვნელობა გაცილებით დიდია სეისმურობის უსაფრთხოების ფაქტორის განსაზღვრასთან შედარებით, რადგანაც ასეთ დაფარვას არ შეუძლია დიდი გადაადგილების ატანა. სწორედ ასეთ შემთხვევაში მიზანშეწონილია სასრულო ელემენტის მეთოდის გამოყენება.
როცა დადგინდება პოტენციალური დანგრევის მექანიზმი, უსაფრთხოების ფაქტორის გამოთვლა შესაძლებელი იქნება ზღვრული წონასწორობის რომელიმე მეთოდით სხვადასხვა კომპიუტერული პროგრამის გამოყენებით, როგორიცაა: FLAC, SLIDE, ROCPLANE და სხვები.
ფერდობის სეისმური მდგრადობის ანგარიში გულისხმობს სტატიკურისაგან განსხვავებით დინამიკური ძაბვებისა და ამ ძაბვების ეფექტის გავლენის ანგარიშს ფერდობის მასალის სიმტკიცეზე.
როდესაც დინამიკური ნორმალური და ძვრის ძაბვები პოტენციალური დანგრევის ზედაპირზე ემატება სტატიკურ ძაბვებს, ამან შეიძლება გამოიწვიოს ფერდობის ინერციული არამდგრადობა. არსებობს ძირითადად ოთხი მეთოდი ფერდობების მდგრადობის ანგარიშისა სეისმურ ზემოქმედებაზე. ორი ამ მეთოდებიდან - ფსევდო-სტატიკური და ნიუმარკის მეთოდები - ფართოდ გამოიყენება პრაქტიკაში. დანარჩენი ორი - მაკდიზი-სიდის და დინამიკური მეთოდები კი - შეზღუდულად.
ყველაზე მარტივი მეთოდი ფერდობების დინამიკური მდგრადობის გაანგარიშებისათვის არის ფსევდო-სტატიკური მეთოდი, რომელშიც სეისმური დატვირთვა შეცვლილია “ექვივალენტური” სტატიკური ჰორიზონტალური აჩქარებით, რომელიც მოქმედებს მეწყერის მასაზე ზღვრულ წონასწორობის ანგარიშებში. ამ მეთოდს ინჟინრები 1920 წლიდან იყენებენ. მისი საშუალებით ხდება უსაფრთხოების ფაქტორის მინიმალური სიდიდის გამოთვლა დაცურების საწინააღმდეგოდ მიმართული სტატიკური ჰორიზონტალური და ვერტიკალური ძალების გათვალისწინებით. ეს ძალები წარმოადგენენ პოტენციალურად დაცურების მასების წონისა და სეისმურობის კოეფიციენტის (ცალცალკე ჰორიზონტალური და ვერტიკალური მდგენელის) ნამრავლს. ჰორიზონტალური ფსევდო-სტატიკური ძალა ამცირებს უსაფრთხოების ფაქტორის მნიშვნელობას დამჭერი ძალის შემცირებასთან და მამოძრავებელი ძალის გაზრდასთან ერთად. ვერტიკალურ ფსევდო-სტატიკურ ძალას ნაკლები გავლენა აქვს დაცვის ფაქტორის მნიშვნელობაზე, მაგრამ მას გარკვეული დადებითი ან უარყოფითი ეფექტის მოხდენა შეუძლია ორივე _ მამოძრავებელ და დამჭერ ძალებზე /2/. ჩვენის აზრით ფსევდო-სტატიკური ანგარიშის დროს დიდი მნიშვნელობა ენიჭება სეისმურობის კოეფიციენტის ჰორიზონტალური და ვერტიკალური მდგენელების განსაზღვრას. ჩვენს ნორმატულ დოკუმენტებში სეისმურობის კოეფიციენტის ვერტიკალური მდგენელის მნიშვნელობა განსაზღვრული არ არის და ფერდობების სეისმური მდგრადობის ანგარიშისთვის სარგებლობდნენ რეკომენდაციებით/9/,რომლის მიხედვით სეისმური ძალის ვერტიკალური მდგენელის გათვალისწინება არ ხდება მისი სიმცირის გამო. ჰორიზონტალური ძალისათვის კი სეისმურობის კოეფიციენტი მიღებულია: 0,01; 0,025; 0,05 და 0.10 _ 6,7,8 და 9 ბალისათვის შესაბამისად. ჩვენის აზრით მიწის ნაგებობის ფერდობების სეისმური მდგრადობისათვის სეისმურობის კოეფიციენტის ვერტიკალური მდგენელის როლი ძალიან იზრდება, რადგანაც მიწის ნაგებობის მდგრადობა განისაზღვრება მისი საკუთარი წონის სიდიდით, რომელიც იცვლება ვერტიკალური რხევის შემთხვევაში. ვერტიკალური მდგენელის სიდიდე განსაკუთრებით აქტუალური ხდება ეპიცენტრალურ ზონასთან ახლოს და მაღალი ნაგებობებისათვის. რადგანაც სეისმურობის კოეფიციენტი წარმოადგენს გრუნტის პიკური აჩქარების ფარდობას სიმძიმის ძალის აჩქარებასთან, მეცნიერებში დღემდე იწვევს დიდ კამათს, პიკური აჩქარების რა წილი მიაკუთვნონ სეისმურობის კოეფიციენტის ჰორიზონტალურ მდგენელს და რა ვერტიკალურს. ამავე დროს ითვლება, რომ პიკური აჩქარების გამოყენებაც დიდი სიფრთხილით უნდა მოხდეს, რადგანაც ეს უკანასკნელი მოქმედებს წამიერად ერთი მიმართულებით და შესაძლებელია მივიღოთ საანგარიშო სეისმური ძალა გადაჭარბებული მნიშვნელობით ან პირიქით. ძირითადად ემპირიული სეისმურობის კოეფიციენტის განსაზღვრა უნდა ემყარებოდეს მეცნიერის პირად გამოცდილებას სპექტრული მრუდის გათვალისწინებით /11/. საერთოდ პიკური აჩქარების განსაზღვრა მიბმული უნდა იყოს ადგილმდებარეობასთან, რასაც საინჟინრო-სეისმოლოგიური კვლევების ჩატარება სჭირდება.
შენიშვნა: სეისმურობის კოეფიციენტის ჰორიზონტალური მდგენელის მნიშვნელობა, რომელიც გამოიყენება პრაქტიკაში, ძირითადად შეესაბამება იმ სიდიდეს, რომელიც ბევრად ნაკლებია, ვიდრე პროგნოზირებადი პიკური აჩქარება. სეისმურობის კოეფიციენტი არ არის ექვივალენტური გრუნტის პიკური აჩქარების სიდიდისა არც ალბათურად და არც დეტერმინისტულად. აქედან გამომდინარე იგი არ უნდა იქნეს გამოყენებული როგორც სეისმურობის კოეფიციენტი ფსევდო-სტატიკურ ანგარიშებში /34/. 1 ცხრილში მოცემულია სეისმურობის კოეფიციენტის ჰორიზონტალური მდგენელის სიდიდეები, რომლებიც რეკომენდებულია გამოყენებისათვის ამერიკასა და იაპონიაში /5/
ცხრილი 1
| სეისმურობისკოეფიციენტის ჰორიზონტალური მდგენელის, kh რეკომენდებული სიდიდე ამერიკასა და იაპონიაში
|
pha არის პიკური ჰორიზონტალური აჩქარება, g-ში
ფსევდო-სტატიკური მეთოდი ფერდობების სეისმური მდგრადობის განსაზღვრისათვის მიუხედავად მისი სიმარტივისა შეიძლება გამოყენებული იყოს მხოლოდ ისეთი ფერდობებისათვის, რომლებიც არ კარგავენ მნიშვნელოვან სიმტკიცეს მიწისძვრის დროს. ამ მეთოდს არ შეუძლია მოახდინოს რეალურად მიწისძვრის რყევით გამოწვეული დინამიკური ეფექტის მთელი კომპლექსის მოდელირება მუდმივი არამიმართული ფსევდო-სტატიკური აჩქარების საშუალებით და იგი რეკომენდებულია ისეთი ფერდობებისათვის, რომლებიც ციკლური დატვირთვის შემთხვევაში არ კარგავენ სიმტკიცის 15%-ზე მეტს /8/. თუ ფერდობი აგებულია ისეთი მასალით, რომელსაც ციკლური დატვირთვისას სიმტკიცის დიდი ნაწილი ეკარგება, ფსევდო-სტატიკური მეთოდით ანგარიშის შემთხვევაში, როცა მაგნიტუდა 6,5-ია, სეისმურობის კოეფიციენტის ჰორიზონტალური მდგენელის მნიშვნელობა უნდა აღებული იქნეს 0,1-ის ტოლი და 8,25 მაგნიტუდის შემთხვევაში კი _ 1,15, რათა გარანტირებული იყოს ფერდობის მდგრადობის შენარჩუნება. არსებობს მაგნიტუდის სხვადასხვა მნიშვნელობისათვის აგებული გრაფიკი, რომლის მიხედვითაც შესაძლებელია განისაზღვროს სეისმურობის კოეფიციენტის ჰორიზონტალური მდგენელი (ნახ.3) /8/
ნახ.3. სეისმურობის კოეფიციენტის ჰორიზონტალური მდგენელის განსაზღვრა მაგნიტუდის მიხედვით
მიუხედავად იმისა, რომ წლების მანძილზე მეცნიერები მუშაობდნენ სეისმურობის კოეფიციენტის ჰორიზონტალური და ვერტიკალური მდგენელის სიდიდის დასადგენად ფსევდო-სტატიკური მეთოდით მიწის ფერდობების სეისმური მდგრადობის ანგარიშისათვის, დისკუსია მათ შორის აქამდე არ წყდება პიკური აჩქარების წილების გადანაწილებაზე სეისმურობის კოეფიციენტის ჰორიზონტალურ და ვერტიკალურ მდგენელებს შორის. /5,6,7/. თუ მოცემულია გრუნტის პიკური ჰორიზონტალური pgah და ვერტიკალური პგავ აჩქარება, რომელიც ეფუძნება სამშენებლო მოედნის სეისმოლოგიურ კვლევებს, როგორ უნდა შეირჩეს სეისმურობის კოეფიციენტი, ან თუ მოცემულია მხოლოდ ერთერთი აჩქარება, როგორ უნდა განისაზღვროს მეორის მნიშვნელობა, გამოყენებული უნდა იყოს მხოლოდ pgah, pgav თუ მათი კომბინაცია და როგორ. ზოგი თვლის, რომ პგავ = 2/3pgah, სეისმურობის კოეფიციენტი კომბინაციაში _ ჰორიზონტალური 2/3pgah, ვერტიკალური 1/3pgav ან 4/9pgah. /7/. ზოგიც მიიჩნევს, რომ იგი უნდა იყოს ტოლი 1/2 ჰორიზონტალური მდგენელისა /1/. ყოველ შემთხვევაში ეს საკითხი პრობლემატურია დღესაც.
თავი 2 - მიწისძვრის შედეგად გრუნტის გათხევადების ეფექტის გავლენა ფერდობების სტატიკურ და სეისმურ მდგრადობაზე
მიწისძვრის შედეგად ფუძის გათხევადებით გამოწვეული მეწყრული მოვლენები ხშირ შემთხვევაში იწვევენ ფერდობების დანგრევას. ქვემოთ ჩამოთვლილია ამერიკაში მომხდარი ზოგიერთი მიწისძვრა, რომელთა მაგნიტუდა არ აღემატება 7 და რომლის შედეგადაც გათხევადებულმა ფუძეებმა გამოიწვია ფერდობების დანგრევა /14/:
- 1925 წ. სანტა-ბარბარა. M=6,3. მიწის კაშხალის დაზიანება. გრუნტი - თიხნარიანი ქვიშა;
- 1940 წ. ელ-ცენტრო, M=7,0. არხის ფერდობის დაზიანება. გრუნტი - დელტის ქვიშა;
- 1950 წ. იმპერიალ ველი. M=5,4. არხის ფერდობის დაზიანება. გრუნტი - დელტის ქვიშა;
- 1954 წ. ანკორიჯი. M=6,7. მიწის დამბის დაზიანება. გრუნტი - ქვიშა.
- 1957წ.სან-ფრანცისკო. M=5,3. ტბის ფერდის დაზიანება. გრუნტი - სანაპიროს ქვიშა.
გარდა ამისა, ცნობილია, რომ 1971 წლის სან-ფერნანდოს მიწისძვრის შედეგად მიწის კაშხალმა კალიფორნიაში განიცადა ზედა ბიეფის ფერდისა და თხემის დიდი დაცურება. საველე კვლევებმა უჩვენა, რომ დაცურება გამოიწვია გათხევადებამ მონალექ ქვიშის ყრილში ზედა ბიეფის პრიზმაში /15/. მონალექ ქვიშიანი ყრილი შედგებოდა მსხვილმარცვლიანი ქვიშის, თიხნარიანი ქვიშის, თიხნარისა და თიხისაგან. პიკური აჩქარებები, რომლებიც ჩაიწერა კაშხალის ძირზე და თხემზე, შეადგენდა 0,48g და 0,55g შესაბამისად. ჩანაწერების ანალიზის შედეგად დადგინდა, რომ დაცურება დაიწყო მიწისძვრით გამოწვეული რხევების შეწყვეტიდან 20-30სეკ. შემდეგ. ასე, რომ დიდი დაცურებითი მოძრაობა განვითარდა სეისმური დატვირთვის გარეშე მხოლოდ კაშხალის წონით გამოწვეული სტატიკური ძაბვების შედეგად. მიწისძვრამდე კაშხალი სტაბილური იყო სტატიკური ძაბვების მიმართ. მას შემდეგ, რაც მიწისძვრა დამთავრდა, ფუძემ ვერ გაუძლო სტატიკურ ძაბვებს და დაინგრა. მთლიანი დრო, რომელიც გავიდა მიწისძვრის დაწყებიდან დიდი დაცურებითი მოძრაობის შეწყვეტამდე, შეადგენდა 2 წუთს. დაცურების შემდგომი დათვალიერებით დადგინდა, რომ პრაქტიკულად მთლიანად გათხევადებულმა გრუნტმა ამ ზონის შიგნით განიცადა ექსტრემალურად დიდი დეფორმაცია.
გათხევადება ისეთი ფენომენია, როდესაც ფუძის მასების ძვრის მედეგობა მცირდება მონოტონური, ციკლური ან დინამიკური განსაზღვრული სიდიდის დატვირთვის ზემოქმედების შედეგად. ამ დროს განვითარებული ხანგრძლივი ძვრის დეფორმაციები იწვევენ ამ მასების დენადობას მანამდე, სანამ ძვრის ძაბვები უფრო მცირეა, ვიდრე შემცირებული ძვრის სიმტკიცე. გათხევადების განსაზღვრა სხვანაირადაც შეიძლება: ძვრის სიმტკიცის დაკარგვა ხდება მაშინ, როცა ფუძის მასები დეფორმირებულია პრაქტიკულად არადრენირებულ მდგომარეობაში და როდესაც მასებზე ზემოქმედებას იწყებს ძვრის ძაბვა და შესაბამისად დეფორმაცია. ამ მასებს შეუძლია გაუძლოს ზედაპირზე ძვრის ძაბვას, როცა ხდება დრენირება, მაგრამ ეს არ მოხდება, თუ საკმარისი საწყისი ძაბვა განვითარებულია არადრენირებულ მდგომარეობაში. მხოლოდ იმ ფუძეებს შეუძლია გამოავლინონ გათხევადების ეფექტის მიმართ ძვრის სიმტკიცე, რომლებსაც უნარი აქვთ მოცულობის შემცირებისა ძვრის ძაბვების ზემოქმედების შემთხვევაში. ამიტომ კუმშვადი ფუძეები არ არიან მგრძნობიარენი გათხევადების ეფექტისადმი, თუ წარმოქმნილი ძვრის ძაბვა ზედაპირზე საკმაოდ დიდი სიდიდის არ არის.
გათხევადება შეიძლება განვითარდეს წყლით გაჯერებულ ქვიშაში, თიხნარში და დენად თიხაში. გათხევადება შეიძლება განვითარდეს აგრეთვე ქვიშის ან თიხნარის ძალიან დიდ მასივში, რომელიც მშრალი და არამკვრივია და ამავე დროს ისეა დატვირთული, რომ ჰაერის გამოდევნა სიცარიელეებიდან შეზღუდულია./16/
ფუძე, რომელზედაც მოქმედებს ციკლური ძვრის ძაბვა, ავლენს სხვადასხვა რეაქციას, რომელიც დამოკიდებულია ფუძის თვისებებზე, ფუძეში არსებულ ძაბვებზე და ციკლური ძაბვების ხანგრძლივობაზე./17/. უმთავრესი მიზეზი ძვრის სიმტკიცის შემცირებისა არის ფოროვანი დაწნევის სიჭარბე გაჯერებულ ფუძეში მიწისძვრის დროს, რადგანაც ჭარბი ფოროვანი დაწნევის დისიპაცია არ ხდება ისე სწრაფად, როგორადაც იგი გროვდება შეჭიდულობის არამქონე მასალაში მაღალი შეღწევადობის უნარით, ამიტომ შედეგად ეს მასალა კარგავს ძვრისადმი სიმტკიცეს.
წყლით გაჯერებული ქვიშის დანალექის გათხევადება ისეთი პროცესია, რომლის დროსაც დინამიკური ძვრის ძაბვები და დეფორმაციები, რომლებიც ვითარდება მიწისძვრის დროს, არღვევს ქვიშის მარცვლებს შორის კონტაქტს. როდესაც გაჯერებულ ფხვიერ ქვიშაზე მოქმედებს ძვრის დატვირთვა, ხდება მისი შემჭიდროვება და წყლის ფოროვანი წნევა იზრდება. ამ დროს მცირდება ეფექტური ძაბვები ფუძეში და ისინი ნულამდე ეცემა. ფუძეს აღარა აქვს ძვრის ძაბვებისადმი მედეგობა და ის გადადის თხიერ მდგომარეობაში. (ეფექტური ძაბვები ის ძაბვებია, რომლებიც უშუალოდ გრუნტის ჩონჩხის ნაწილაკებისაგან გადაეცემა ნაწილაკებს და რომლებიც ცვლიან გრუნტის მასის მოცულობას და იწვევენ გრუნტში შინაგან ხახუნს).გათხევადება ძირითადად ვითარდება 0,075-0,20 მმ-ის ზომის მარცვლებიან ქვიშაში.
ძაბვები, რომლებიც მოქმედებენ წყალგაჯერებულ ქვიშის მასის შიგნით, იყოფა ორ ტიპად:
- ძაბვები, რომლებიც გადაეცემა უშუალოდ გრუნტის ჩონჩხის ნაწილაკებისაგან ნაწილაკებს;
- ძაბვები, რომლებიც მოქმედებენ სითხის შიგნით, რომლითაც შევსებულია ფორები.
პირველი, როგორც უკვე ავღნიშნეთ, წარმოადგენს ეფექტურ ძაბვებს, მეორე კი – ფოროვანი დაწნევაა ან ნეიტრალური ძაბვა. მხოლოდ ეფექტურ ძაბვებს შეუძლია შეცვალოს გრუნტის მასის მოცულობა და მხოლოდ ეს ძაბვები იწვევენ გრუნტში შინაგან ხახუნს.
სრული დაწნევა p, რომელიც შედგება ეფექტური p’ და ფოროვანი uw დაწნევისაგან იქნება
- p = p’ + uw (1)
- აქ p’ = z γ , სადაც z არის შეტივტივებული გრუნტის სისქე; γ არის შეტივტივებული გრუნტის მოცულობითი წონა.
- γ = (γg - γw) (2)
მიწისძვრის დროს გრუნტის ჰორიზონტალურ დანალექზე მოქმედი ძალები მოცემულია ნახ.3. ვერტიკალური და ჰორიზონტალური ეფექტური ძაბვები, რომლებიც მოქმედებენ დანალექზე, აღნიშნულია σz და k0σz-ით. აღნიშნავს გრუნტის დაწნევის კოეფიციენტს მშვიდ მდგომარეობაში. ძვრის ძაბვები, რომლებიც წარმოიქმნება განივი ბრტყელი ტალღებისაგან, აღნიშნულია τ–თი.
როგორც ითქვა, თუ წყლის ფოროვანი დაწნევა ფუძის შეუმჭიდროებულ მასაში იზრდება იმ დრომდე, როცა ის გაუტოლდება გარედან მოდებულ დაწნევას, ასეთ შემთხვევაში შეიძლება ითქვას, რომ ფუძე გაწყლოვანდა თუ გათხევადება განვითარდა ფუძის მასის იმ ზონაში, რომელიც მთლიანად შემოზღუდული არ არის სხვა ტიპის დანალექით, შედეგად გვექნება გრუნტის მასების ჰორიზონტალური დაცურება ჩაუმაგრებელი ზედაპირის მიმართულებით.
ნახ.4. გრუნტის ზედაპირის ქვეშ დანალექზე მოსული დატვირთვა და მიწისძვრის შედეგად მასში განვითარებული ძვრის დეფორმაცია
თუ მოძრაობა ფარდობითად მცირეა მცურავი მასების ზომებთან შედარებით, მაშინ მივიღებთ გათხევადებით გამოწვეულ მეწყერს, რასაც თან ერთვის გრუნტის დაჯდომა და ბზარების გაჩენა. ეს ყველაფერი შეიძლება განვითარდეს მიწისძვრის დროს ქვიშის ფენებში, რომლებიც დევს სტაბილური ფუძის მასების ქვეშ /14/. ქვიშის ფენის გათხევადების შესაძლებლობა განისაზღვრება ქვიშის საწყისი მდგომარეობით, მიწისძვრის დროს აღძრული ციკლური ძაბვების სიდიდით, ქვიშაში მიწისძვრამდე არსებული საწყისი ძაბვებით და ქვიშის ფენების დისიპაციის უნარით. გათხევადების განვითარებისათვის მიწისძვრის დროს განსაკუთრებულ ინტერესს იწვევს ციკლური ძაბვის კოეფიციენტი τ/σ’0–ის ცოდნა. აქ τ არის ძვრის ძაბვის შეფარდება საწყის ნორმალურ ეფექტურ ძაბვასთან, σ’0-თან. შემჩნეულია, რომ რაც უფრო დიდია ეს შეფარდება ციკლური ძაბვების მოდებამდე, მით უფრო მეტია გათხევადებისაგან განვითარებული სირთულეები.
ციკლური ძაბვის კოეფიციენტი ისაზღვრება შემდეგნაირად /18.19.20/:
- τ/σ’0 = 0,65 rd amax σ0/σ’0 g (3)
- აქ amax არის მაქსიმალური აჩქარება გრუნტის ზედაპირზე;
- σ0 არის მთლიანი ზედაპირული დაწნევა ქვიშის ფენაზე განხილულ მდგომარეობისათვის;
- σ’0 არის საწყისი ეფექტური დაწნევა ქვიშის ფენაზე განხილული მდგომარეობოსათვის;
- rd არის ძაბვის შემცირების ფაქტორი 1-დან გრუნტის ზედაპირიდან 0,9-მდე 9 მ-ის სიღრმეში:
- rd=1-0,015d (4)
- d არის სიღრმე მეტრებში
- 0,65 მიუთითებს, რომ τ არის აბსოლუტური ძვრის ძაბვების 65%.
ციკლების რიცხვი დამოკიდებულია მიწისძვრის ხანგრძლივობაზე და მაგნიტუდაზე. თუ მაგნიტუდა M=7, ციკლების საჭირო რიცხვი იქნება 10; თუ M=7,5, ციკლების საჭირო რიცხვი იქნება 20; და თუ M=8, მაშინ ციკლების რიცხვი იქნება 30.
კრიტიკული ციკლური ძაბვის კოეფიციენტი, რომელიც საჭიროა 100%-ანი ფოროვანი დაწნევის კოეფიციენტის განსაზღვრისათვის, შეიძლება გამოითვალოს ან ლაბორატორიული ციკლური გამოცდების შედეგად ან კორელაციით სტანდარტული პენეტრაციის მაჩვენებლის SPT(N1)60-ს მიხედვით. ემპირიული მეთოდი გამოიყენება საველე პირობებში გათხევადების ეფექტის დასახასიათებლად, რაც გამოწვეულია ბუნებრივი მიწისძვრებით ან აფეთქებებით. ეს მეთოდი ემყარება მთელ მსოფლიოში ადრე მომხდარი მიწისძვრების შედეგად ქვიშის დანალექის გათხევადების მდგომარეობის შესწავლას და ლოკალურ ტერიტორიაზე იყენებს SPT(N1)60 გრაფიკს, რომელიც სხვა არაფერია, თუ არა ემპირიული გრაფიკი, რომელიც გვაძლევს განსხვავებას ფუძის გათხევადების შესაძლებლობასა და არშესაძლებლობას შორის. მის მახასიათებლად ითვლება სტანდარტული პენეტრაციის მედეგობის კრიტიკული სიდიდე, Nკრიტ. რომელიც განსაზღვრულია როგორც SPT სიდიდე გარკვეულ სიღრმეზე, რომელიც არ იცვლება მიწისძვრამდე და მის შემდეგ. ზოგი მას განსაზღვრავს, როგორც ზღვარს მსუბუქ და მძიმე დაზიანებებს შორის ნაგებობის ფუძეში (50 სმ-ზე მეტი ჯდენა ან 1o –ით შემობრუნება / 18 /). იმ ქვეყნებში, სადაც არ არსებობს პრაქტიკული მონაცემები, კრიტიკული შPთ(N1)60 გრაფიკი ჩადებულია სამშენებლო კოდებში, კერძოდ აშშ-ში, ჩინეთში, იაპონიაში. SPT პროცედურის ღირებულება მის სიმარტივეშია და იგი განიხილება უმეტესი ინჟინრების მიერ როგორც საუკეთესო მეთოდი დღესდღეობით გათხევადებისადმი მედეგობის განსაზღვრისათვის. სტანდარტული პენეტრაციის მაჩვენებელი SPT წარმოადგენს მნიშვნელოვან ბაზას ფუძის გათხევადების ეფექტის პოტენციალის განსაზღვრისათვის და იგი ფართოდ გამოიყენება გაჯერებული ფუძის დანალექში გათხევადებისადმი მედეგობის შესაფასებლად. ამ პროცედურით გათხევადების კონტროლის ფაქტორის კორელაცია უკეთესად ხდება, ვიდრე ფარდობითი სიმკვრივით. ერთადერთი კრიტიკული საკითხია ის, რომ მეთოდი არ განიხილავს არც ფოროვანი დაწნევის განვითარების საკითხს და არც დატვირთვის ხანგრძლივობას. სიდიდე არ გამოიყენება ღორღიანი ქვიშისათვის და იგი არც მგრძნობიარეა წარსულში განვითარებულ დეფორმაციებისადმი.
სტანდარტული პენეტრაციის მედეგობა, SPT, რომელიც აცალკავებს გათხევადებისა და არგათხევადების მდგომარეობას 1,5 მ-ის სიღრმეზე, გამოითვლება შემდეგნაირად / 24 /:
- Nკრიტ. = N [1+0,125(ds-3)–0,05(dw–2)] (5)
- სადაც ds არის განხილულ ადგილას ქვიშის ფენის სისქე, მ-ში;
- dw არის გრუნტის ზედაპირის ქვეშ წყლის დონის სიღრმე, მ-ში.
- N არის ინტენსიურობაზე დამოკიდებული ფუნქცია, რომელიც მოყვანილია 2 ცხრილში.
ცხრილი 2;
| მოდიფიცირებული მერკალის სკალა | დარტყმა 30 სმ2-ზე |
|---|---|
| VII | 6 |
| VIII | 10 |
| IX | 16 |
ნახ 5,a-ზე მოცემულია სტანდარტული პენეტრაციის მაჩვენებლის მრუდები /24,25/, რომელებიც გვიჩვენებენ ემპირიულ დამოკიდებულებას ქვიშის შესაძლო გათხევადებასა და SPT დარტყმების რიცხვს შორის ქვიშის სიწმინდის მიხედვით 7,5 მაგნიტუდისათვის. აბსცისაზე გვაქვს SPT დარტყმების რიცხვი შესწორებული ეფექტური ზედაპირული დაწნევით 1ტ/30სმ2-ზე უროსათვის 60%-ანი თავისუფალი ვარდნის ენერგიისათვის ანუ ფუძის სიმტკიცე. ციკლური ძაბვის კოეფიციენტი, τav /σ’0, რომელიც საჭიროა 100%-ანი ფოროვანი დაწნევის კოეფიციენტისათვის, ანუ გრუნტის მოძრაობის ინტენსიურობა, მოცემულია ორდინატაზე. τav არის ექვივალენტური მუდმივი ციკლური განივი ძაბვისა, რომელიც ჩნდება მიწისძვრის დროს. σ’0 არის ვერტიკალური ეფექტური ძაბვა. ამიტომ საჭიროა ჯერ განისაზღვროს ციკლური ძაბვის კოეფიციენტი გრუნტის რომელიმე სიღრმეზე ისეთ გრუნტებში, რომელიც შეიძლება გათხევადდეს და შემდეგ განივი ძაბვა, გამოწვეული მიწისძვრისაგან, უნდა შედარდეს განივ ძაბვასთან, რომელიც იწვევს გათხევადებას.
ციკლური ძაბვის კოეფიციენტი მაგნიტუდის სხვა მნიშვნელობისათვის შეიძლება მიღებული იქნას 7,5 მაგნიტუდის მრუდის რეგულირებით 3 ცხრილში მოცემული სიდიდეების გამოყენებით. (ნახ.5,b). / 24,27 /
ცხრილი 3
| მიწისძვრის მაგნიტუდა | 0,65max-სთვის საჭირო ციკლების რაოდენობა | მარეგულირებელი ფაქტორი |
|---|---|---|
| 8,5 | 26 | 0,89 |
| 7,5 | 15 | 1,0 |
| 6,75 | 10 | 1,13 |
| 6,0 | 5 | 1,32 |
| 5,25 | 2-3 | 1,5 |
საერთოდ დადასტურებულია ჯებირებისა და მიწის კაშხალების 2 აშკარად გამოხატული ტიპი ქცევისა მიწისძვრის დროს: 1. ფხვიერი საშუალო სიმკვრივემდე ქვიშის ფერდობები, რომლებიც მგრძნობიარენი არიან ცალკეული დატვირთვით გამოწვეული ფოროვანი დაწნევის გაზრდის მიმართ, რასაც შედეგად მოჰყვება ძვრისადმი სიმტკიცის შემცირება და პოტენციალურად დიდი მოძრაობა, მთლიანად ინგრევიან და 2. შეჭიდულობის უნარიანი თიხის, მშრალი და ზოგიერთი სიმკვრივის ქვიშის შემთხვევაში ფოროვანი დაწნევის გაზრდის პოტენციალი დაბალია, ამიტომ ციკლური დეფორმაციებიც ჩვეულებრივად მცირეა და გრუნტის მასა ინარჩუნებს მისი სტატიკური არადრენირებული ძვრისადმი მედეგობის დიდ ნაწილს /8/.
სხვადასხვა ქვეყნებში მიწისძვრების შედეგად მიწის ჯებირებისა და კაშხალების ქცევის შესწავლის შედეგად გაკეთებულია შემდეგი დასკვნები /12/:
- უმეტესი მონალექყრილიანი კაშხალები მრავალი წლის განმავლობაში ინარჩუნებენ მდგრადობას და თუ მათი ფერდობები აგებულია ზომიერი ქანობით კარგ ფუნდამენტზე, ისინი გაუძლებენ საშუალოდ ძლიერ რყევას დაახლოებით 0,2g აჩქარებით, მიწისძვრის მაგნიტუდით 6,5-7 შესამჩნევი დაზიანების გარეშე.
- კარგად აგებული კაშხალი გაუძლებს საშუალო მიწისძვრის რყევას პიკური აჩქარებით 0,2 g დაზიანების ეფექტის გარეშე.
- კაშხალებს,რომლებიც აგებული არიან თიხის გრუნტით თიხიან ან კლდოვან ფუნდამენტზე, შეუძლიათ გაუძლონ ძლიერ მიწისძვრებს აჩქარებით 0,35 g-0,8 g–მდე, მაგნიტუდით 8,25, შესამჩნევი დაზიანების გარეშე.
- კაშხალებისათვის, რომლებიც აგებულია გაჯერებული შეჭიდულობის არამქონე გრუნტით და განიცდიან ძლიერ რყევას, დაზიანების მთავარი მიზეზი არის წყლის ფოროვანი დაწნევის გაზრდა და სიმტკიცის დაკარგვა, რაც შეიძლება განვითარდეს წყლის ფოროვანი დაწნევის შედეგად. ასეთი კაშხალებისათვის ფსევდო-სტატიკური ანგარიშის მეთოდის გამოყენება სიფრთხილით უნდა მოხდეს.
- ზოგიერთი კაშხალი დაინგრა მიწისძვრის შემდგომ 24 საათში, რაც იმაზე მიუთითებს, რომ კაშხალის გრუნტის მოძრაობა, გამოწვეული ფილტრაციით ნაპრალებში, ხდება მიწისძვრის რყევის შედეგად და ეს არის მიზეზი დანგრევისა. ამიტომ საჭიროა შესაბამისი ფილტრების მოწყობა კაშხალებში სეისმურ რეგიონებში, რათა არ განვითარდეს პროგრესულად ეროზია და წყალმა არ შეაღწიოს ნაპრალებში.
შენიშვნა: დინამიკური ანგარიშების ჩასატარებლად მაღალი კაშხალების საერთაშორისო კომისიის მიწისძვრების კომიტეტი იძლევა შემდეგ რეკომენდაციას: მაღალი ჯებირების კაშხალები, რომელთა დაზიანებას შეუძლია გამოიწვიოს მსხვერპლი ან დიდი ნგრევა, უნდა გაანგარიშებული იყოს ფსევდო-სტატიკური მეთოდით, რათა შემდგომ გამოკვლეული იყოს ის ნაკლი, რომელიც შეიძლება წარმოიქმნას ამ მეთოდით ანგარიშის დროს. დაბალი კაშხალებისათვის იგივე კომიტეტი იძლევა რეკომენდაციას, რომ ანგარიშის დროს გამოყენებული უნდა იქნეს სეისმურობის კოეფიციენტის ჰორიზონტალური მდგენელის მუდმივი სიდიდე. ამავე დროს ეს კომიტეტი მიუთითებს, რომ მიწისძვრით გამოწვეული ჰორიზონტალური აჩქარება იცვლება კაშხალის სიმაღლის მიხედვით და ანგარიში გამყარებული უნდა იქნეს მოდელური გამოცდებით./8/
ნახ.5. დამოკიდებულება გათხევადების ეფექტის გამომწვევი ციკლური ძაბვის კოეფიციენტსა და SPT(N1)60—ის მნიშვნელობას შორის ა)M=7,5 და ბ) სხვადასხვა მაგნიტუდისათვის.
თავი 3 - ფერდობების სტატიკური მდგრადობის განსაზღვრისათვის გამოყენებული საანგარიშო მეთოდები
ზღვრული წონასწორობის მეთოდი
ფერდობის სტატიკური მდგრადობის ხარისხის განმსაზღვრელად მიღებულია მდგრადობის მარაგის კოეფიციენტი, ანუ უსაფრთხოების ფაქტორი, F, რომელიც წარმოადგენს სიდიდეს პოტენციალური ძვრისადმი წინაღობის ძალების ფარდობისა იმ აქტიურ ძალებთან, რომლებსაც შეუძლიათ გამოიწვიონ გრუნტის დაცურება. მისი გამოთვლა შესაძლებელია ძვრის სიმტკიცის, S, შეფარდებით წონასწორობისთვის საჭირო ძვრის ძაბვასთან, τ.
- F = S / τ = c’ + (σ -u) tan φ’ (6)
- აქ c’ არის შეჭიდულობა;
- φ’ არის ხახუნის კუთხე;
- σ არის ჩამონგრევის სიბრტყის მთლიანი ნორმალური ძაბვა;
- u არის წყლის ფოროვანი დაწნევა;
(σ -u) არის ეფექტური ნირმალური ძაბვა დანგრევის სიბრტყეში.
უსაფრთხოების ფაქტორის გამოთვლა ხორციელდება ზღვრული წონასწორობის სხვადასხვა მეთოდის საშუალებით სტატიკური წონასწორობის ერთი ან მეტი განტოლების გამოყენებით, იმ გრუნტის მასების დაყოფით ვერტიკალური ბლოკების სასრულო რიცხვით, რომლებიც განთავსებულია დაცურების ზედაპირის ზემოთ. ამ მეთოდებში არსებობს 2 ტიპის გადაწყვეტა: “გამარტივებული”,რომელშიც სტატიკური წონასწორობის მდგომარეობა მკაცრად არ კმაყოფილდება და დაშვებები კეთდება მარტივი ფორმით ანგარიშის მისაღებად და “ზუსტი”, რომელშიც წონასწორობის მდგომარეობა მთლიანად კმაყოფილდება დასაშვები სიდიდით /4/.
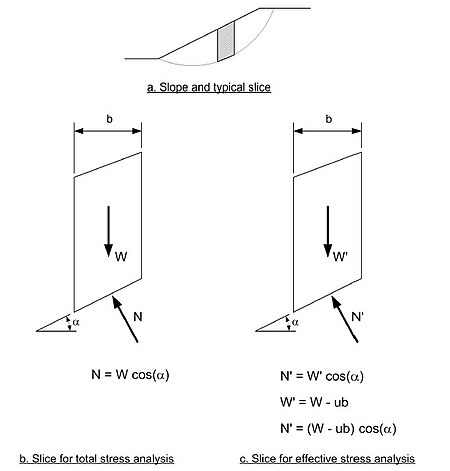
ძალები, რომლებიც ჩვეულებრივად მოქმედებენ ინდივიდუალურად ბლოკზე, მოცემულია ნახ. -ზე.
- აქ W არის ბლოკის წონა;
- E არის ჰორიზონტალური (ნორმალური) ძალები ბლოკის გვერდებზე;
- X არის ვერტიკალური (ძვრის) ძალები ბლოკებს შორის
ნახ.6. ტიპური ბლოკი და ძალები ბლოკთა მეთოდისათვის
- N არის ნორმალური ძალა ბლოკის ძირში;
- S არის ძვრის ძალა ბლოკის ძირში.
გარდა ბლოკის წონისა, ყველა ძალა უცნობია და ისინი ისე უნდა გამოითვალოს, რომ დაკმაყოფილდეს სტატიკური წონასწორობა.
ძვრის ძალა, S, ბლოკის ძირში პირდაპირ არ განიხილება როგორც უცნობი წონასწორობის განტოლებაში და მისი გამოსახვა შესაძლებელია სხვა ცნობილი და უცნობი სიდიდეებით ასე:
- S= τΔl (7)
- სადაც τ არის ძვრის ძაბვა;
- Δl არის ბლოკის ძირის სიგრძე
ნორმალური ძალა, N, ტოლია ნორმალური ძაბვის, σ, ნამრავლისა ბლოკის ძირის, Δl, სიგრძეზე, ანუ
- N = σ Δl (8)
- (6)-დან ისაზღვრება τ
- τ = c’ + (σ -u) tan φ’ / F (9)
- მაშინ
- S = c’ Δl / F + (N-uΔl) tan φ’ /F (10)
ამგვარად ძვრის ძალის განსაზღვრა შეიძლება მოხდეს (9)-დან. დანარჩენი უცნობები და ძალები, რომლებიც უნდა განისაზღვროს წონასწორობის განტოლებიდან, მოცემულია 4 ცხრილში.
ცხრილი 4
უცნობები და განტოლებები ზღვრული წონასწორობის მეთოდისათვის
|
იმისათვის, რომ დამყარდეს ბალანსი უცნობების რიცხვსა და წონასწორობის განტოლებების რიცხვს შორის (როგორც 4 ცხრილიდან ჩანს, განტოლებების რიცხვი 3n ნაკლებია უცნობების რიცხვზე (5n-2)-ზე, საჭიროა გაკეთდეს ზოგიერთი დაშვება, რათა მოხდეს ამოცანის გადაწყვეტა. ეს დაშვებებია:
- უსაფრთხოების ფაქტორის სიდიდე მუდმივია დაცურების ზედაპირის გასწვრივ, თუმცა ფაქტიურად ეს ასე არ არის.
- ყველა ზღვრული წონასწორობის მეთოდი თხოულობს პოტენციალური დაცურების ზედაპირის მოხაზულობის განსაზღვრას უსაფრთხოების ფაქტორის მიხედვით. ამ მოხაზულობის შერჩევა გრძელდება მანამდე, სანამ არ განისაზღვრება დაცვის ფაქტორის მინიმალური სიდიდე. ანგარიშის გამარტივებისათვის დაცურების ზედაპირს განსაზღვრავენ როგორც წრიულს ან შედგენილს მცირე სწორი ხაზებისაგან.
- წრიული დაცურების ზედაპირი ხშირად გამოიყენება, რადგანაც ის მოხერხებულია წრის ცენტრის მიმართ მომენტების შეჯამებისათვის, ამავე დროს ასეთი ზედაპირი ამარტივებს ანგარიშებს.
ბლოკების ჩვეულებრივი მეთოდი
მეთოდი განავითარა ფელენიუსმა (1936) და ზოგჯერ მას „ფელენიუსის“ მეთოდი ეწოდება. ამ მეთოდის მიხედვით ბლოკის გვერდებზე მოქმედი ძალები უგულებელყოფილია (ნახ.7). ნორმალური ძალა ბლოკის ფუძეზე გამოითვლება ძალების ჯამით ბლოკის ძირის პერპენდიკულარული მიმართულებით. როცა ნორმალური ძალა გამოითვლება, მომენტები შეჯამდება წრის ცენტრის გარშემო, რათა განისაზღვროს უსაფრთხოების ფაქტორი. ნახ.-ზე მოცემული ბლოკისათვის და ძალებისათვის უსაფრთხოების ფაქტორი შემდეგნაირად გამოითვლება: /3/
- F =Σ [c’ Δl + (Wcosα – u Δl cos2α ) tan φ’ ] / ΣWsin α (11)
- სადაც c’ და φ’ არის ძვრის სიმტკიცის პარამეტრები ბლოკის ძირის ცენტრის მიმართ;
- W არის ბლოკის წონა;
- α არის ბლოკის ძირის დახრის კუთხე;
- u არის წყლის ფოროვანი დაწნევა ბლოკის ძირის ცენტრის მიმართ;
- Δl არის ბლოკის ძირის სიგრძე.
5 ცხრილში მოცემულია უცნობებისა და განტოლებების რიცხვი, რომელიც საჭიროა ამ მეთოდისათვის.
ცხრილი 5
უცნობები და განტოლებები ფელენიუსის მეთოდისათვის
|
ნახ.7. ტიპური ბლოკი და ძალები ბლოკების ჩვეულებრივი მეთოდისათვის a) ფერდობი და ტიპური ბლოკი; b) ბლოკი მთლიანი ძაბვების საანგარიშოდ; c) ბლოკი ეფექტური ძაბვების საანგარიშოდ.
ამ მეთოდში ბლოკის გვერდებზე მოქმედი ძალები უგულვებელყოფილია. მეთოდი აგრეთვე არ აკმაყოფილებს ძალების წონასწორობის პირობას არც ვერტიკალური და არც ჰორიზონტალური მიმართულებით. მომენტთა წონასწორობა კმაყოფილდება მთლიანი მასისათვის დაცურების ზედაპირის ზემოთ, მაგრამ არა ინდივიდუალურად ბლოკისათვის. ამ მეთოდით გამოთვლილი უსაფრთხოების ფაქტორი შეიძლება თითქმის 20%-ით განსხვავდებოდეს ზუსტი მეთოდით გამოთვლილი მნიშვნელობიდან. ეს მეთოდი გამოიყენება მხოლოდ დაცურების წრიული მოხაზულობისათვის. სიმარტივის გამო ამ მეთოდით ანგარიში კალკულატორითაც შეიძლება.
ბიშოფის გამარტივებული მეთოდი
მეთოდი განავითარა ბიშოფმა (1955) და იგი ეფუძნება იმ დაშვებას, რომ ბლოკებს შორის ძალები, E, ჰორიზონტალურია (ნახ. 8). დაცურების ზედაპირი მიღებულია წრიულად. მოქმედი ძალები ჯამდება ვერტიკალური მიმართულებით. უსაფრთხოების ფაქტორი მიიღება შემდეგი გამოსახულებით: /3/
- F = { Σ [c’Δ x + (W+Pcosβ –u Δxsecα )tan φ’] / mα } / Σ Wsin α – Mp/R (12)
- აქ Δx არის ბლოკის სიგანე და mα განისაზღვრება შემდეგი განტოლებით:
- mα = cosα + sinα tan φ’/F (13)
- აქ P არის წყლის ძალის ტოლქმედი, რომელიც მოქმედებს ბლოკის წვერზე;
- Mp არის შესაბამისად მისი მომენტი. დანარჩენი ცნობილია ნახაზიდან.
უსაფრთხოების ფაქტორი, გამოთვლილი (11)-დან, აკმაყოფილებს ძალების წონასწორობას ვერტიკალური მიმართულებით და მომენტების წონასწორობას წრის ცენტრის გარშემო. უცნობები და განტოლებები ბიშოფის გამარტივებული მეთოდისათვის მოცემულია 6 ცხრილში.
ცხრილი 6
უცნობები და განტოლებები ბიშიფის გამარტივებული მეთოდისათვის
|
ამ მეთოდით ძალების ჰორიზონტალური წონასწორობა სრულად არ კმაყოფილდება, ამიტომ ამ მეთოდის გამოყენება ფსევდო-სტატიკური გაანგარიშებისათვის, სადაც დამატებითი ჰორიზონტალური ძალებია მოდებული, კითხვის ქვეშაა. თუ ნაგებობა დაპროექტებულია ამ მეთოდით, საბოლოო ანგარიში უნდა შემოწმდეს სპენსერის მეთოდით.
ნახ.8. ტიპური ბლოკი და ძალები ბიშოფის გამარტივებული მეთოდისათვის a) ფერდობი და ტიპური დაცურების ზედაპირი; b) ტიპური ბლოკი.
სპენსერის მეთოდი
ამ მეთოდის მიხედვით ბლოკზე მოქმედი გვერდული ძალები პარალელურია. მაგალითად, ყველა გვერდული ძალა დახრილია ერთი და იგივე კუთხით. ნორმალური ძალა ბლოკის ძირზე მოქმედებს ძირის ცენტრში - ეს დაშვება მცირე გავლენას ახდენს საბოლოო ანგარიშზე. მეთოდი სრულად აკმაყოფილებს როგორც ძალის, ასევე მომენტის წონასწორობის მოთხოვნას. ამ მეთოდის გამოყენება სასურველია სტატიკური მდგრადობის სრული ანგარიშისათვის და როგორც მაკონტროლებელი ფერდობების მდგრადობის მარტივი მეთოდებით ანგარიშისას. ნახ.9-ზე მოცემულია ტიპური ბლოკთაშორისი საზღვარი AB, და ძალები, რომლებიც მოქმედებენ მასზე. მთლიანი ბლოკთაშორისი ძალა, Z, მოქმედებს θ კუთხით ჰორიზონტალურ ღერძთან და იგი არის ტოლქმედი შემდეგი 3 ძალისა: ნორმალური ეფექტური ძაბვით გამოწვეული პ’ძალის;ძვრის ძალის S/Fv = 1/Fv(c’H + p’tanφ’) = Zsin θ , სადაც Fv არის უსაფრ φ’არის ხახუნის კუთხე ეფექტურ ძაბვასთან მიმართებაში, c’არის შეჭიდულობა ეფექტურ ძაბვასთან მიმართებაში; და ფოროვანი წყლის დაწნევით გამოწვეული, W, ძალის. თუ დავუშვებთ ფოროვანი წყლის დაწნევის თანაბარ განაწილებას, მაშინ B-სთან ეს დაწნევა ტოლი იქნება B=ruγH-სა, სადაც γ არის ფუძის სიმკვრივე, H არის ბლოკთაშორისი საზღვრის, AB, სიმაღლე და ru არის ფოროვანი დაწნევის კოეფიციენტი. W=1/2ruH2 . /23/
უსაფრთხოების ფაქტორის განსაზღვრა ხდება შემდეგნაირად:
- Fv =1/zsinθ [c’H +tan φ’(zcosθ – 1/2 ruγH2)] (15)
უცნობები და განტოლებები, რომელიც გამოიყენება ამ მეთოდში, მოცემულია 7 ცხრილში.
ნახ.9. ბლოკთაშორის საზღვარზე მოქმედი ძალები სპენსერის მეთოდისათვის
ცხრილი 7
უცნობები და განტოლებები სპენსერის მეთოდისათვის
|
სპენსერის მეთოდი (1967) შეიძლება გამოყენებული იქნეს არაწრიული დაცურების ზედაპირისთვისაც. მეთოდი თხოულობს აუცილებლად კომპიუტერულ პროგრამას ანგარიშისათვის, რადგანაც მომენტისა და ძალის წონასწორობა უნდა დაკმაყოფილდეს ყოველი ბლოკისათვის და ანგარიში გრძელდება უსაფრთხოების ფაქტორის განსაზღვრის მცდელობათა გარკვეული რიცხვისათვის და ბლოკთაშორისი ძალების დახრის განსაზღვრისათვის.
ძალთა წონასწორობის მეთოდი მოდიფიცირებულ შვედურ მეთოდთან ერთად
ამ მეთოდის მიხედვით კმაყოფილდება ძალთა წონასწორობა ორივე - ჰორიზონტალური და ვერტიკალური მიმართულებით, მაგრამ არ კმაყოფილდება მომენტთა წონასწორობის პირობა. ეს მეთოდი ეფუძნება ძალთა დახრის კუთხის, θ-ს, დაშვებას ბლოკებს შორის (ნახ.10) უცნობებისა და განტოლებების რიცხვი მოყვანილია 8 ცხრილში /3/:
ნახ.10-ზე მოცემული zi და zi+1 სიდიდეები წარმოადგენენ ძალებს ბლოკისათვის ფერდობის ზემოთ და ქვემოთ მიმართულებით. θ არის ბლოკთაშორისი ძალების დახრის კუთხე.
ნახ. 10. ტიპური ბლოკი და ძალები მოდიფიცირებული შვედური მეთოდისათვის ბლოკთაშორისი ძალების, θ, სავარაუდო მიმართულება.
ცხრილი 8.
უცნობები და განტოლებები ძალთა წონასწორობის მეთოდისათვის
|
ძალების გამოთვლა იწყება პირველი ბლოკიდან, სადაც zi=0 და პროცესი გრძელდება ყველა ბლოკისათვის ბოლო ბლოკის ჩათვლით. ანგარიში წარმოებს ფერდობის წვერიდან ძირისაკენ. ბლოკთაშორისი ძალის zi+1-ის მნიშვნელობა ფერდობის ბოლო ბლოკისათვის (დაცურების ზედაპირის ძირი) იქნება ნული, თუ უსაფრთხოების ფაქტორის მნიშვნელობა სწორად არის განსაზღვრული. თუ ეს ძალა არ არის ნულის ტოლი, მაშინ უნდა შეირჩეს უსაფრთხოების ფაქტორის ახალი სიდიდე და პროცესი განმეორდეს მანამ, ვიდრე ამ ძალის მნიშვნელობა 0-ს არ გაუტოლდება.
ამ მეთოდისათვის დამახასიათებელია ის, რომ ბლოკთაშორისი ძალების დახრის კუთხის მიმართ უსაფრთხოების ფაქტორი მგრძნობიარეა, მისი მნიშვნელობა შეიძლება მივიღოთ გადაჭარბებული ან შემცირებული მნიშვნელობით. ძალთა წონასწორობის მეთოდი ერთადერთია ზღვრული წონასწორობის მეთოდებს შორის, რომელიც შეიძლება გამოყენებული იქნეს არაწრიული დაცურების ზედაპირისათვის. ეს მეთოდი გაცილებით მარტივია სპენსერის მეთოდთან შედარებით, მაგრამ სიზუსტეში მას ჩამოუვარდება. ეს ორი მეთოდი იძლევა იდენტურ შედეგებს, თუ გამოყენებული იქნება გვერდული ძალების დახრის კუთხის ერთი და იგივე მნიშვნელობა.
ჯანბუს ბლოკების განზოგადოებული მეთოდი
ამ მეთოდში /4/ დაშვებულია n რიცხვი ნორმალური ძალის, N, და (n-1) რიცხვი ბლოკთაშორისი ძალის, E-ს, მოდების წერტილისა. რადგანაც ამ შემთხვევაში 1 დაშვებით მეტია, ვიდრე საჭიროა, აქედან გამომდინარე, ტექნიკურად ზუსტი გადაწყვეტის მიღება არ ხდება. ამ მეთოდში ბოლო ძალის, N-ის, პოზიცია არ გამოიყენება და მომენტის წონასწორობა ბოლო ბლოკისათვის არ კმაყოფილდება.
მორგენშტერნისა და პრაისის მეთოდი
ამ მეთოდში /4/ დაშვებულია n რიცხვი N ძალის მოდების წერტილისა და (n-1) რიცხვი ბლოკთაშორისი ჰორიზონტალური, E, და ვერტიკალური, X, ძალებს შორის ფარდობითი კავშირისა. როცა ანგარიშში უსასრულოდ მცირე ბლოკია გამოყენებული, ნ მიისწრაფის უსასრულობისაკენ, მაგრამ პრინციპები იგივე რჩება. რადგანაც კეთდება 1-ზე მეტი დაშვება, ვიდრე მოთხოვნილია, შემოყვანილია ზედმეტი უცნობი და ამიტომ სტატიკური წონასწორობა კმაყოფილდება ზუსტად.
სარმას მეთოდი
განიხილება პოტენციალური დაცურების მასების წონასწორობა. დაცურების მასებიდაკავშირებულია ABCD დაცურების ხაზთან და იყოფა ნ ვერტიკალურ ბლოკად. ნახ.11-ზე მოცემულია I ბლოკი და მასზე მოქმედი ძალები. ნორმალური ძალა Ni ითვლება მოდებულად ბლოკის შუა წერტილში. უნდა გამოითვალოს კრიტიკული ჰორიზონტალური აჩქარება, რომელიც საჭიროა თავისუფალ ზედაპირთან დაკავშირებული ფუძის მასების ზღვრულ წონასწორობის მდგომარეობაში ყოფნისათვის. აქედან გამომდინარე ეს აჩქარება არის საზომი უსაფრთხოების ფაქტორისა /35/. ბლოკის ვერტიკალური და ჰორიზონტალური წონასწორობიდან მიღებულია შემდეგი გამოსახულებები:
- Ni cosαi + Ti sin αi = Wi - DXi (16)
- Ti cosαi - Ni sinαi = KWi + DEi (17)
იგულისხმება, რომ KWi ძალის მოქმედებით ზედაპირზე მობილიზებულია სრული ძვრის სიმტკიცე, რაც იმას ნიშნავს, რომ უსაფრთხოების ფაქტორი ტოლია 1-ს და აქედან გამომდინარე K წარმოადგენს კრიტიკულ აჩქარებას როგორც საკუთარი წონის აჩქარების ნაწილს. მთლიანი მასების სრული წონასწორობისათვის დაკმაყოფილებული უნდა იქნეს მომენტის წონასწორობის პირობა. სირთულე მდგომარეობს ბლოკთაშორისი ძალების Xi-ის განაწილების დადაგენაში. საპოვნელია X ძალების ის მნიშვნელობები, რომლებიც დააკმაყოფილებენ წონასწორობის განტოლებებს. ითვლება, რომ ცნობილია ამ ძალების განაწილების ფორმა და არა მათი სიდიდეები. უსაფრთხოების ფაქტორი, FLi, ბლოკის ვერტიკალურ ნაწილში (მაგ. უსაფრთხოების ლოკალური ფაქტორი) შეიძლება გამოითვალოს ასე:
- FLi = [(Ei – PWi) tan φi + ciHi] / Xi (18)
სადაც tan φi და ci არის i სექციის საშუალო ძვრის სიმტკიცის პარამეტრი.
უსაფრთხოების ფაქტორის სიდიდე, რომელიც იძლევა ნულოვან კრიტიკულ აჩქარებას, არის უსაფრთხოების ფაქტორი, რომელიც მიღებულია სეისმური ზემოქმედების გარეშე.
ნახ.11. ტიპური ბლოკი და მასზე მოქმედი ძალები სარმას მეთოდისათვის
წარწერები ნახაზზე:
- Ei და Ei+1 არის ჰორიზონტალური ძალვა i და i+1 ბლოკის ვერტიკალურ გვერდებზე, გამოხატული ეფექტურ ძალებში;
- Xi და Xi+1 არის ძვრის ძალა i და i+1 ბლოკის ვერტიკალურ გვერდებზე, შესაბამისად;
- Pwi და Pwi+1 არის ბლოკის ვერტიკალურ i და i+1 გვერდებზე მოქმედი წყლის დაწნევის ტოლქმედი, შესაბამისად;
- Wi არის ბლოკის წონა;
- Ni არის ბლოკ 1-ზე მოქმედი ბლოკის სიმძიმის ცენტრში მოდებული ჰორიზონტალური ძალა;
- ui არის ბლოკის ფუძეზე მოქმედი ნორმალური ძალა, გამოხატული ეფექტურ ძაბვებში;
- Ni არის ბლოკის ფუძეზე მოქმედი ფოროვანი დაწნევით გამოწვეული ძალა;
- Ti არის ბლოკის ძვრის ძალა;
- zi დაცურების ხაზის ზემოთ Ei ძალის მოდების წერტილის სიმაღლე;
- ci და φi არის ბლოკის ფუძის მასალის ეფექტური ძვრის სიმტკიცის პარამეტრები;
- Ni = N’i + ui,
- Ei = E’i + Pwi;
- Hi არის ი-ური ნაწილის დაცურების მასების სიმაღლე;
- Kc არის კრიტიკული ჰორიზონტალური აჩქარება, როგორც ნაწილი სიმძიმის ძალის აჩქარებისა, რომელიც საჭიროა :დაცურების ხაზის ზემოთ მდებარე მასების ზღვრული წონასწორობის მდგომარეობაში შესანარჩუნებლად;
- h არის ბლოკის სიგანე
- αi არის BC ხაზის მიერ შექმნილი კუთხე ჰორიზონტთან;
- xi და yi არის ბლოკის ძირის საშუალო წერტილის კოორდინატები ღერძების მიმართ;
- xg და yg არის დაცურებული მასების სიმძიმის ცერტრის კოორდინატები ღერძების მიმართ;
- DEi =Ei+1 -Ei;
- DXi = Xi+1 –Xi;
შენიშვნა: ზემოთ მოყვანილ მეთოდებში გათვალისწინებულია წონასწორობის ყველა პირობის დაკმაყოფილება წინასწარ მიღებული დაშვებებით. ბიშოფის მოდიფიცირებული მეთოდი, მართალია, არ აკმაყოფილებს წონასწორობის ყველა პირობას, მაგრამ საკმაოდ ზუსტია მხოლოდ დაცურების წრიული ზედაპირისათვის. ყველა დანარჩენი მეთოდებით შეიძლება განისაზღვროს ნებისმიერი დაცურების ზედაპირის უსაფრთხოების ფაქტორის სიდიდე, ოღონდ სირთულეები დაკავშირებულია შესაბამისი ძალების განაწილების შერჩევასთან მორგენშტერნისა და პრაისის და სარმას მეთოდებში, აგრეთვე რიცხვითი არასტაბილურობის ხშირ პრობლემასთან, რაც გვხვდება ჯანბუს განზოგადებულ მეთოდში. ამიტომ ამ მეთოდების გამოყენება მოუხერხებელია საინჟინრო პრაქტიკისათვის. ნებისმიერი მოხაზულობის დაცურების ზედაპირისათვის უმჯობესია გამოყენებული იქნეს სპენსერის მეთოდი, ხოლო ბიშოფის მოდიფიცირებული მეთოდი - წრიული დაცურების ზედაპირისათვის. თუ მდგრადობის ანგარიშები ჩატარებულია სხვა მეთოდებით, საჭიროა სტატიკური უსაფრთხოების ფაქტორი კრიტიკული დაცურების ზედაპირისათვის შემოწმდეს სპენსერის ან ბიშოფის მეთოდებით /33/.
სასრულო ელემენტის მეთოდი
თუ საჭიროა სასრულო ელემენტის მეთოდით უსაფრთხოების ფაქტორის იმ სიდიდის განსაზღვრა, რომელიც ექვივალენტური იქნება ზღვრული წონასწორობის მეთოდით გამოთვლილისა, უნდა ჩატარდეს შემდეგი ოპერაციები: /3/
- სასრულო ელემენტის მეთოდით გაანგარიშებული უნდა იქნეს ძაბვები ფერდობისათვის;
- ამორჩეული უნდა იქნეს საცდელი დაცურების ზედაპირი;
- დაცურების ზედაპირი უნდა დაიყოს სეგმენტებად;
- გამოითვალოს ნორმალური და ძვრის ძაბვები შერჩეული დაცურების ზედაპირის გასწვრივ;
- გამოყენებული უნდა იყოს ნორმალური ძაბვებისა და ძვრისადმი სიმტკიცის პარამეტრები c’ და φ’, რათა განისაზღვროს საჭირო სიმტკიცე ძვრისადმი დაცურების ზედაპირის გასწვრივ წერტილებში;
- გამოითვალოს მთლიანი უსაფრთხოების ფაქტორი შემდეგნაირად:
- F = Σ siΔl /Στi Δl (15)
- სადაც si არის შესაბამისი ძვრისადმი სიმტკიცე;
- τi არის ძვრის ძაბვა;
- Δl არის სეგმენტებად დაყოფილი დაცურების ზედაპირის თითოეული სეგმენტის სიგრძე.
კვლევებმა აჩვენა, რომ უსაფრთხოების ფაქტორის მნიშვნელობა, რომელიც გამოითვლება ზემოთ მოყვანილი მიმდევრობით, იდენტურია იმ უსაფრთხოების ფაქტორის მნიშვნელობისა, რომელიც გამოითვალა ზღვრული წონასწორობის ზუსტი მეთოდებით.
ლოკალური უსაფრთხოების ფაქტორის გამოთვლა შესაძლებელია ძაბვებისა და ძვრის სიმტკიცის მნიშვნელობებით ფერდობის შერჩეულ წერტილში. ლოკალურად გამოთვლილი უსაფრთხოების ფაქტორის მნიშვნელობა შეიძლება უფრო დაბალი იყოს, ვიდრე (15) ტოლობიდან ან ზღვრული წონასწორობის მეთოდიდან გამოთვლილი მთლიანი მინიმალური უსაფრთხოების ფაქტორი. ლოკალური ფაქტორის მნიშვნელობა 1-ზე ნაკლები ჯერ კიდევ არ მიუთითებს ფერდობის არასტაბილურობაზე. ძაბვები გადანაწილებული იქნება დაზიანების ერთი წერტილიდან მეორე წერტილამდე, სადაც უსაფრთხოების ფაქტორი 1-ზე მეტი იქნება. ამ შემთხვევაში ფერდობი იქნება სტაბილური.
თავი 4 - ფერდობების სეისმური მდგრადობის განსაზღვრისათვის გამოყენებული საანგარიშო მეთოდები
ფერდობების სეისმური მდგრადობის ანგარიში ითვალისწინებს ორი დამატებითი ფაქტორის განსაზღვრას: 1. დინამიკური ძაბვების გამოთვლას, რომელსაც იწვევს მიწისძვრა და 2. აღძრული დინამიკური ძაბვების გავლენას ფერდობის დაძაბულ მდგომარეობაზე და ფერდობის მასალის სიმტკიცეზე. როდესაც დინამიკური ნორმალური და ძვრის ძაბვები პოტენციალურ დანგრევის ზედაპირზე ემატება სტატიკურ ძაბვებს და ძვრის ძაბვები გადააჭარბებენ ფუძის ძვრისადმი სიმტკიცეს, ამან შეიძლება გამოიწვიოს ფერდობის ინერციული არასტაბილურობა. პრობლემა შეიძლება გადაიჭრას ან ფსევდო-სტატიკური ანგარიშის მეთოდით ან მიწისძვრის რყევით გამოწვეული ფერდობის პერმანენტული გადაადგილების განსაზღვრით.
ფსევდო-სტატიკური (PS) მეთოდი
უმეტესი წილი რეკომენდაციებისა და კოდებისა, როგორიცაა მაგალითად BSI 1995, FHWA 1997 და სხვა, ფერდობების სეისმური მდგრადობის განსაზღვრისათვის გვთავაზობენ მარტივ ფსევდო-სტატიკურ (PS) ანგარიშებს როგორც სტანდარტულ პროცედურას. ამ ანგარიშებში გათხევადების საკითხები არ არის აქტუალური. ფსევდო-სტატიკური მიდგომა არის სტანდარტული ზღვრული წონასწორობის მეთოდით ფერდობების სტატიკური მდგრადობის ანგარიშების განზოგადებისა, რომელშიც სეისმური ეფექტი წარმოდგენილია როგორც ტანზე მოქმედი დამატებითი ძალა, რომელიც იძლევა სეისმურ ეფექტს და რომელშიც გათვალისწინებულია სეისმურობის კოეფიციენტი, განსაზღვრული კოდებიდან სეისმურ ინფორმაციაზე დაყრდნობით. PS ძალას ძირითადად გულისხმობენ მიმართულს ჰორიზონტალურად, მაგრამ მას შეიძლება ვერტიკალური მიმართულებაც ჰქონდეს, რაც აუცილებლად უნდა აისახოს სეისმურობის კოეფიციენტის მნიშვნელობაში.
მეთოდი იძლევა უსაფრთხოების ფაქტორის მინიმალური სიდიდის განსაზღვრას ფერდობის დაცურების საწინააღმდეგო სტატიკური ჰორიზონტალური და ვერტიკალური ძალების გათვალისწინებით, რაც გამოიხატება ჰორიზონტალური კჰ და კვ ვერტიკალური სეისმურობის კოეფიციენტის ნამრავლით დაცურების მასების წონაზე. (ნახ.12). ფსევდო-სტატიკური მეთოდი ფერდობების სეისმური მდგრადობის განსაზღვრისათვის მიუხედავად მისი სიმარტივისა, შეიძლება გამოყენებული იქნას მხოლოდ ისეთი ფერდობებისათვის, რომლებიც არ კარგავენ მნიშვნელოვან სიმტკიცეს 15%-ზე მეტს ციკლური დატვირთვის შემთხვევაში. ასეთი ფუძეები არიან: თიხები, თიხნარიანი, მშრალი და ნესტიანი შეჭიდულობის გარეშე და მკვრივი შეჭიდულობის გარეშე ფუძეები. შესაბამისი სეისმურობის კოეფიციენტის შერჩევა ძალიან მნიშვნელოვანია და რთული. თეორიულად სეისმურობის კოეფიციენტის სიდიდე დამოკიდებულია ინერციული ძალის ამპლიტუდის სიდიდეზე. რადგანაც მიწის ფერდობი არ არის ხისტი და მიწისძვრის დროს წარმოქმნილი პიკური აჩქარება მოქმედებს ძალიან მოკლე დროში, სეისმურობის კოეფიციენტი, რომელიც გამოიყენება პრაქტიკაში, ძირითადად შეესაბამება აჩქარების ისეთ სიდიდეს, რაც ბევრად დაბალია, ვიდრე პროგნოზირებადი პიკური აჩქარება. არ არსებობს სეისმურობის კოეფიციენტის შესარჩევად რაიმე სპეციფიკური წესი. შერჩევის სხვადასხვა კრიტერიუმი გვთავაზობს, რომ სეისმურობის კოეფიციენტი დაფუძნებული უნდა იყოს აჩქარების მოსალოდნელ დონეზე დაცურების მასების შიგნით და უნდა შეესაბამებოდეს მოსალოდნელი პიკური აჩქარების დონეს.
ნახ.12 ფსევდო-სტატიკური ანგარიშის მეთოდი ჰორიზონტალური აქსელეროგრამით
როდესაც სტატიკური ანგარიშით განსაზღვრულია ფერდობის რღვევის ზედაპირი და სტატიკური უსაფრთხოების ფაქტორი, ამის შემდეგ შესაძლებელია სხვადასხვა აქსელეროგრამის ზემოქმედება რღვევის ზედაპირზე დინამიკური ძაბვების მისაღებად ამ ზედაპირის გასწვრივ. შესაძლო საანგარიშო სქემა ფერდობის მდგრადობის ანალიზისათვის სასრულო ელემენტის ან სასრულო სხვაობის მეთოდით მოცემულია ნახ.13-ზე. სხვაობა სტატიკურსა და დინამიკურ ძაბვებს შორის შესაძლებელია შემდეგ გამოყენებული იქნას სეისმურობის კოეფიციენტის დროში ცვლილების განსასაზღვრავად /5/. ანგარიშში შეყვანილი უნდა იქნას თვით ნაგებობის სიმაღლე, ნაგებობის და მისი ფუნდამენტის განივი ტალღის სიჩქარეები, ფერდობის დაქანება და შემავალი აქსელეროგრამა, რომელიც მოდებული უნდა იყოს ფუნდამენტის ძირზე, რომელიც განლაგებულია გრუნტის ძირითადი ფენის ზემოთ. ნახ.14-ზე მოცემულია სეისმურობის კოეფიციენტის გამოთვლის მეთოდოლოგია.
ნახ.13. ფერდობის სეისმური მდგრადობის ანგარიშისათვის გამოყენებული შესაძლო საანგარიშო სქემა
ნახ.14. სეისმურობის კოეფიციენტის გამოთვლისათვის გამოყენებული მეთოდოლოგია
მარტო ჰორიზონტალური აქსელეროგრამის გამოყენება იძლევა ვერტიკალური სეისმურობის კოეფიციენტის მცირე სიდიდეს. ამიტომ ანგარიშში გათვალისწინებული უნდა იყოს აქსელეროგრამის ვერტიკალური მდგენელიც, რათა მიღებული იქნას სეისმურობის კოეფიციენტის ის მნიშვნელობა, რომელიც აუცილებელია ფერდობის სეისმური სტაბილურობისათვის.
არსებობს ისეთი მოსაზრებაც, რომ ფერდობის ფსევდო-სტატიკური მდგრადობის პრობლემა შეიძლება გარდაიქმნას ექვივალენტურ სტატიკურ პრობლემად ფერდობის მოდიფიცირებული გეომეტრიით და ხვედრითი წონით /21/. მსგავსება ფსევდო-სტატიკურ და სტატიკურ პრობლემას შორის იძლევა საშუალებას ფარდობითად კარგად განვითარებული სტატიკური ანგარიშებიდან ნაკლებად განვითარებულ ფსევდო-სტატიკურ ანგარიშებზე გადასვლისა. ეს მეთოდი გამოსაყენებელია ნაკლები შეჭიდულობის მქონე მასალის შემთხვევაში, რათა ჩატარდეს სრული ანგარიშები მიწისძვრის შემთხვევაში გაჭიმვისაგან გამოწვეული ბზარის პრევენციის კრიტერიუმის დასადგენად და კრიტიკული ღრმა დაცურების ზედაპირის შემთხვევაში ზღვრული ანგარიშების ჩასატარებლად. ნახ.15-ზე მოცემულია ბაზისური ფსევდო-სტატიკური პრობლემა.
ნახ.15 ფერდობის ფსევდო-სტატიკური მდგრადობის პრობლემა
ნახ. 16a-ზე მოცემულია ბაზისური ფსევდო-სტატიკური პრობლემის შემდეგნაირი წარმოდგენა: დიფერენცირებული dE და dW ტოლქმედის ვექტორი აღნიშნულია dP–თი, რომლის დახრის კუთხე ვერტიკალთან იქნება θ. შემოტანილია ახალი კოორდინატთა სისტემა (X,Y), რომელიც შემობრუნებული θ კუთხით საწყისი (x,y) სისტემის მიმართ მანამდე, ვიდრე X კოორდინატა არ გახდება ჰორიზონტალური. (ნახ.16b). ნახ.15ზე და 16b-ზე არის მხოლოდ სხვადასხვანაირად წარმოდგენილი ერთი და იგივე ფერდობის მდგრადობის პრობლემა (გაერთიანებული ძალები და კოორდინატთა სისტემის ცვლა არ ახდენს ეფექტს ფიზიკურ პრობლემაზე). ნახ.16b–ზე მოცემულია სტანდარტული სტატიკური პრობლემა შეცვლილი გრუნტის ხვედრითი წონით და ფერდობის გეომეტრიით. ამ სტატიკური პრობლემის ამოხსნა იძლევა იგივე შედეგებს (იგივე მინიმალური უსაფრთხოების ფაქტორს და დაცურების კრიტიკულ ზედაპირს), როგორსაც საწყისი ფსევდო-სტატიკური პრობლემა ნახ.15-დან. მიღებულია, რომ იდენტურობა სამართლიანია ყველა არაჰომოგენური ამოცანისათვის პირობითი გეომეტრიით, გარე დატვირთვით და ფოროვანი დაწნევის განაწილებით; აგრეთვე სამართლიანია ყველა ზღვრული წონასწორობის მეთოდისათვის.
ნახ16a. ფერდობის ტანზე მოქმედი ძალთა კომბინაცია
ნახ16b. კოორდინატთა სისტემის შემობრუნება
შედეგად სტატიკური პრობლემა, რომელიც იდენტურია მოცემული ფსევდო-სტატიკური პრობლემისა, გამოიხატება ასე:
- θ = arctan { kh / 1± kv} (16)
- γ’ = γ (1±kv) / cosθ (17)
- β’ = β + θ (18)
- H’ = H sin β’ / sinβ (19)
აქ kh და kv არის სეისმურობის კოეფიციენტის ჰორიზონტალური და ვერტიკალური მდგენელი შესაბამისად. kv–ს დადებითი მნიშვნელობა ნიშნავს, რომ PS ძალის კომპონენტა მოქმედებს სიმძიმის ძალის მიმართულებით. /21/.
პერმანენტული დეფორმაციის მეთოდი
ნიუმარკის მეთოდი
XX საუკუნის ბოლო დეკადაში ფერდობების სეისმური მდგრადობის განსაზღვრისათვის ხშირად იყენებდნენ პერმანენტულ დეფორმაციის მეთოდს, რომელიც დაამუშავა ნიუმარკმა 1965 წ /22/. მასში განვითარებულია კონცეფცია, რომ მიწისძვრის ეფექტი ფერდობების მდგრადობისათვის უნდა განისაზღვროს უფრო დეფორმაციების გათვალისწინებით, ვიდრე მინიმალური უსაფრთხოების ფაქტორით. მეთოდში ნაგულისხმევია ფერდობების ხისტ-პლასტიური მასალა და აჩქარების დროში ცვლილება მიწისძვრის დროს. თუ ინერციის ძალები, რომლებიც მოქმედებენ პოტენციალურ დანგრევის მასებზე (სტატიკა + დინამიკა) აჭარბებენ არსებულ მედეგობის ძალებს და უსაფრთხოების ფაქტორი 1-ზე ნაკლებია, მაშინ პოტენციალური დანგრევის მასები დიდხანს ვერ შეინარჩუნებენ წონასწორობას. ნიუმარკმა გამოიყენა დახრილი სიბრტყეზე ბლოკების მედეგობის ანალოგია, რათა განევითარებინა ფერდობის პერმანენტული გადაადგილების პროგნოზირების მეთოდი (ნახ.17). თუ ბლოკის წონა არის W, მაშინ უსაფრთხოების ფაქტორი სტატიკური წონასწორობის მდგომარეობით (ნახ.15) განისაზღვრება ასე:
- F = tanφ / tanβ (20)
- სადაც φ არის ხახუნის კუთხე.
ნახ.17 ანალოგია პოტენციალურ მეწყერსა (a) და დახრილ სიბრტყეზე ბლოკის მდგომარეობას შორის (b)
ნახ.18. ძალები, რომლებიც მოქმედებენ ბლოკზე დახრილ სიბრტყეში სტატიკურ მდგომარეობაში (a) და დინამიკურ მდგომარეობაში (b)
მიწისძვრის შემთხვევაში რომელიღაც გარკვეულ დროში ჰორიზონტალური აჩქარება დახრილ სიბრტყეზე ტოლი იქნება:
- ah (t) = kh(t)g (21)
სადაც kh არის სეისმურობის კოეფიციენტის ჰორიზონტალური მდგენელი. ვერტიკალური მდგენელი არ გაითვალისწინება.
სეისმური უსაფრთხოების ფაქტორი გამოითვლება შემდეგნაირად:
- Fs = [cosβ –kh(t)sinβ ] tanφz / [sinβ +kh(t)cosβ] (22)
მაკდიზი-სიდის მეთოდი
მეთოდი (1978) იძლევა საშუალებას მიწის ნაგებობის ფერდობების პერმანენტული დეფორმაციის პროგნოზირებისა მიწისძვრის დროს და ეფუძნება ნიუმარკის მეთოდს /8,22/. მასში გამოყენებულია განივი კოჭის ანგარიში სეისმურ დატვირთვაზე ნაგებობის დინამიკური რეაქციის შესასწავლად (ნახ.19) და იგი წარმოადგენს ზღვრული წონასწორობის პრინციპებზე დაფუძნებული ანგარიშის ალტერნატივას, იყენებს საშუალო აჩქარებას, რომელიც დაკავშირებულია პოტენციალური დანგრევის ზედაპირის სიღრმესთან ნახ.20) და ნორმალიზებულ პერმანენტულ გადაადგილებას აკავშირებს მიღებულ აჩქარებასთან სხვადასხვა მაგნიტუდის მიწისძვრების შემთხვევაში (ნახ.21). სასრულო ელემენტის მეთოდი გამოყენებული იყო მიწის ჯებირების ორგანზომილებიანი რეაქციის შესასწავლად, კერძოდ შესწავლილი იყო შეფილდის კაშხალის დანგრევის მექანიზმი 1925 წლის სანტა-ბარბარას მიწისძვრის შედეგად და გაანალიზებული იყო სან-ფერნანდოს კაშხალის ქცევა 1971 წლის მიწისძვრის შედეგად.
ნახ.19. საშუალო აჩქარების გამოთვლა სასრულო-ელემენტიანი რეაქციის ანალიზის მიხედვით (n არის ელემენტების რიცხვი დაცურების ზედაპირის გასწვრივ)
ნახ20. მაქსიმალურიაჩქარების კოეფიციენტის ვარიაციები დაცურების მასების სიღრმის მიხედვით
ნახ.21. საშუალო ნორმალიზებული გადაადგილების ვარიაციები მიღებული აჩქარების მიხედვით
შენიშვნა: 1. ის ფერდობები, რომელთაც ფსევდო-სტატიკური გაანგარიშებით უსაფრთხოების ფაქტორი მუდმივი სეისმურობის კოეფიციენტის გამოყენებით მეტი აქვთ 1,1-ზე, შეიძლება ჩაითვალონ მდგრადად. თუ ფსევდო-სტატიკური გაანგარიშებით უსაფრთხოების ფაქტორი ნაკლებია 1,1-ზე, მაშინ დამპროექტებელმა ინჟინერმა უნდა გაიანგარიშოს ან ნიუმარკის მეთოდით ან სხვა რომელიმე მეთოდით ფერდობის გადაადგილების სიდიდე და გაითვალისწინოს დანგრევის საფრთხის შესამცირებელი საშუალებები.
ნიუმარკის მეთოდით გამოთვლილი ფერდობის გადაადგილება თუ 10 სმ-ზე ნაკლებია, ნაკლებად სავარაუდოა, რომ მეწყერის სერიოზული დაძვრა ან ფერდობის დანგრევა მოხდეს. 10÷100სმ-ის დიაპაზონში ფერდობის დეფორმაციამ შეიძლება გამოიწვიოს საკმაოდ სერიოზული გრუნტის დაბზარვა და სიმტკიცის საკმარისი დაკარგვა იმისათვის, რომ განვითარდეს მიწისძვრის შემდგომი ნგრევა. ამ დროს პროფესიონალმა დამპროექტებელმა უნდა განსაზღვროს ამ დიაპაზონში გადაადგილების რომელი სიდიდე იქნება უსაფრთხო. ამავე დროს უნდა გაითვალისწინოს მეწყერის გეომეტრია და მასალის თვისებები. 100 სმ-ზე სიდიდის გადაადგილება ნამდვილად გამოიწვევს მეწყერის დამანგრეველ მოძრაობას და ასეთი ფერდობი განხილული უნდა იქნეს არამდგრადად /34/.
ფსევდო-სტატიკურ ანგარიშებში ჰორიზონტალური სეისმურობის კოეფოციენტის kh მნიშვნელობა აღებული უნდა იქნეს 0,5PGA (გრუნტის პიკური აჩქარება), ხოლო ვერტიკალური სეისმურობის კოეფიციენტი კვ - ნულის ტოლი გამოყენებული უნდა იყოს იმ შემთხვევაში, როდესაც ფერდობის სეისმური მდგრადობა განიხილება გათხევადების გარეშე. ამ შემთხვევაში უსაფრთხოების საძიებო ფაქტორი F ტოლი უნდა იყოს 1,1-ის. ხანგრძლივი მიწისძვრების შემთხვევაში kh აღებული უნდა იყოს 0,33 PGA./36/
2. ზოგადად ფსევდო-სტატიკური მეთოდით განსაზღვრული დაცურების კრიტიკული ზედაპირი გაცილებით ღრმაა სტატიკური გაანგარიშებით მიღებულთან შედარებით და მისი საზღვრები დამოკიდებულია Ns = c/(γH)-ის სიდიდეზე. აქ ც არის გრუნტის შეჭიდულობა; γ არის გრუნტის ხვედრითი წონა; H არის ფერდობის სიმაღლე. ნახ.22-ზე მოცემულია ბიშოფის მეთოდით სტატიკური და ფსევდო-სტატიკური მეთოდით განსაზღვრული დაცურების კრიტიკული ზედაპირების საზღვრები ფერდობისათვის დახრის კუთხით α=45ო და გრუნტის ხახუნის კუთხით 20o./40/
ნახ.22. ფერდობის სტატიკური და ფსევდო-სტატიკური დაცურების კრიტიკული ზედაპირის მოხაზულობა
თავი 5 - ფერდობების სეისმური მდგრადობის გაანგარიშება EN 1998-1:2004 და EN 1998-5:2004-ის მიხედვით
ევროპული სტანდარტი /28,29/ მომზადებული იყო ტექნიკური კომიტეტის CEN/TC 250-ის მიერ, რომლის სამდივნო პასუხისმგებელია ყველა კონსტრუქციის ევროკოდზე. ამ ევროპულ სტანდარტს უნდა მიეცეს ეროვნული სტანდარტის სტატუსი ან იდენტური ტექსტის გამოქვეყნებით ან მხარდაჭერით არა უგვიანეს 2005 წლის ივნისისა და ყველა წინააღმდეგობა ეროვნულ სტანდარტში უნდა აღმოიფხვრას არა უგვიანეს 2010 წლის მარტისა. ამ პირობის შესრულებაზე შეთანხმდნენ შემდეგი ევროპული ქვეყნები: ავსტრია, ბელგია, კვიპროსი, ჩეხეთი, დანია, ესტონეთი, ფინეთი, საფრანგეთი, გერმანია, საბერძნეთი, უნგრეთი ირლანდია, ისლანდია, იტალია, ლატვია, ლიტვა. ლუქსემბურგი, მალტა, ნიდერლანდები, ნორვეგია, პოლონეთი, პორტუგალია, სლოვაკია, სლოვენია ესპანეთი, შვედეთი, შვეიცარია და გაერთიანებული სამეფო.
ევროპის ქვეყნები აღიიარებენ, რომ ევროკოდი სასარგებლოა როგორც სახელმძღვანელო დოკუმენტი.
ევროკოდისათვის გამოსაყენებელი ეროვნული სტანდარტები უნდა შეიცავდეს სრულ ტექსტს ევროკოდისა (ეროვნულ დანართან ერთად). ეროვნული დანართი შეიძლება შეიცავდეს მხოლოდ ინფორმაციას იმ პარამეტრებზე, რომლებიც ღიაა ევროკოდში ეროვნული არჩევანისათვის. ეს პარამეტრებია:
- სიდიდეები ან კლასები, რომელთა ალტერნატივა მოცემულია ევროკოდში;
- სიდიდეები, რომლებიც გამოიყენება ქვეყანაში და რომელთა მხოლოდ სიმბოლოებია მოცემული ევროკოდში;
- პროცედურა, რომელიც გამოიყენება ქვეყანაში და რომლის ალტერნატივა მოცემულია ევროკოდში;
გარდა ამისა შეიძლება მიღებული იყოს ეროვნული დანართში ინფორმაციული დამატების შეტანის გადაწყვეტილება. აგრეთვე შეიძლება იყოს ასეთ დამატებით ინფორმაციაზე განმარტება, რაც ხელს შეუწყობს მომხმარებელს ევროკოდის გამოყენებაში.
საანგარიშო სეისმური ზემოქმედების განსაზღვრა
გრუნტის მდგრადობის შემოწმება უნდა ჩატარდეს იმ შემთხვევაში, თუ საჭიროა საანგარიშო სეისმური ზემოქმედების შემთხვევაში ბუნებრივი და ხელოვნური ფერდობის ახლოს მშენებარე ნაგებობის უსაფრთხოების და/ან საექსპლოტაციო საიმედოობის უზრუნველყოფა. ფერდობების ზღვრული წონასწორობა ამ შემთხვევისათვის განისაზღვრება ისეთი მდგომარეობით, რომლის მიღმა ვითარდება გრუნტის მასების მოულოდნელი დიდი პერმანენტული გადაადგილებები ფერდობის სიღრმეში.
ფერდობების რეაქცია საანგარიშო სეისმურ ზემოქმედებაზე შეიძლება გამოანგარიშებული იყოს ან დინამიკურ ანალიზში მიღებული მეთოდებით, როგორიცაა სასრულო ელემენტებისა და ხისტი ბლოკების მოდელი ან გამარტივებული ფსევდო-სტატიკური მეთოდით. ეს უკანასკნელი შემდეგი შეზღუდვებით უნდა განხორციელდეს: ზედაპირის ტოპოგრაფია და ფუძის სტრატიგრაფია არ უნდა იყოს მკვეთრად არარეგულარული და გრუნტებში არ უნდა ვითარდებოდეს წყლის დიდი ფოროვანი დაწნევა. ციკლური დატვირთვის შემთხვევაში ფერდობის გრუნტმა არ უნდა დაკარგოს მნიშვნელოვანი სიხისტე.
საანგარიშო სეისმური ინერციული ძალები FH და FV, რომლებიც მოქმედებენ გრუნტის მასებზე ჰორიზონტალური და ვერტიკალური მიმართულებით, ფსევდო-სტატიკურ ანგარიშებში შემდეგნაირად გამოითვლება: /29/
- FH = 0,5 a S.W (23)
- FV = ± 0,5FH თუ avg / ag მეტია 0,6 (24)
- FV = ±0,33 FH თუ avg / ag არ არის მეტი 0,6-ზე (25)
სადაც a არის A ტიპის გრუნტის (ცხრილი 12) ag აჩქარების შეფარდება სიმძიმის ძალის g აჩქარებასთან;
- avg არის გრუნტის საანგარიშო აჩქარება ვერტიკალური მიმართულებით;
- ag არის გრუნტის საანგარიშო აჩქარება A ტიპის გრუნტისათვის;
- W არის დაცურებული გრუნტის მასის წონა;
- S არის გრუნტის პარამეტრი, რომლის მნიშვნელობა მოცემულია 9 და 10 ცხრილებში და დამოკიდებულია იმაზე, თუ რომელი ტიპის დრეკადი რეაქციის სპექტრი იქნება გამოყენებული.
თუ მიწისძვრა, რომელსაც სამშენებლო მოედნის სეისმური საფრთხის ალბათურ შეფასებაში უმეტესი წვლილი შეაქვს და ხასიათდება იმით, რომ ზედაპირული ტალღის გავრცელების მაგნიტუდა, Ms, არ აღემატება 5,5-ს, მაშინ რეკომენდებულია II ტიპის დრეკადი რეაქციის სპექტრის გამოყენება (ნახ.25), წიმააღმდეგ შემთხვევაში კი უნდა გამოყენებული იქნეს I ტიპის რეაქციის სპექტრი (ნახ.24)
შენიშვნა: Ms არის ზედაპირული ტალღის მაგნიტუდა, ტოლი მაქსიმალური ურთიერთ პერპენდიკულარული ჰორიზონტალური გადაადგილების ამპლიტუდის ტოლქმედის მარტივი ლოგარითმისა, გაზომილი მიკრონებში, 20 წმ-ანი პერიოდის ზედაპირული ტალღებისათვის.
სეისმური ზემოქმედების ჰორიზონტალური მდგენელისათვის დრეკადი რეაქციის სპექტრი Se (T) განისაზღვრება შემდეგი გამოსახულებით (ნახ.23) /29/
- 0 ≤ T ≤ TB : Se (T) = ag S [1 + T/ TB (η 2,5 – 1)] (26)
- TB≤ T≤ TC : Se (T) = ag S η 2,5 (27)
- TC ≤ T ≤ TD : Se (T) = ag S η 2,5 [TC / TD ] (28)
- TD ≤ T ≤ 4s : Se (T) = ag S η 2,5 [TC TD /T2 ] (29)
- სადაც Se (T) არის დრეკადი რეაქციის სპექტრი;
- T წრფივი, ერთი თავისუფლების ხარისხის მქონე სისტემის რხევის პერიოდი;
- TB არის სპექტრული აჩქარების მრუდის მუდმივი მონაკვეთის შესაბამისი პერიოდის ზედა ზღვარი;
- TC არის სპექტრული აჩქარების მრუდის მუდმივი მონაკვეთის შესაბამისი პერიოდის ქვედა ზღვარი;
- TD განსაზღვრავს სპექტრის მუდმივი გადაადგილების რეაქციის დასაწყისის სიდიდეს;
- ag არის AA ტიპის გრუნტის საანგარიშო აჩქარება (ag =γ1 agR )
- S არის გრუნტის პარამეტრი;
- η არის ჩაქრობის შემასწორებელი კოეფიციენტი, რომლის ბაზური მნიშვნელობა 5%-ანი ბლანტი ჩაქრობის შემთხვევისათვიის ტოლია 1,0-ს.
ზემოთ მოყვანილი მნიშვნელობები განსაზღვრავენ დრეკადი სპექტრის მოხაზულობას და დამოკიდებულია გრუნტის ტიპზე. (ცხრილი 12)
ნახ.23.დრეკადი რეაქციის სპექტრი
ცხრილი9. რეკომენდებული 1 ტიპის დრეკადი რეაქციის სპექტრის პარამეტრების მნიშვნელობები
| გრუნტის ტიპი | S | TB(s) | Tc(s) | Td(s) |
|---|---|---|---|---|
| A | 1,0 | 0,15 | 0,4 | 2,0 |
| B | 1,2 | 0,15 | 0,5 | 2,0 |
| C | 0,15 | 0,20 | 0,6 | 2,0 |
| D | 1,35 | 0,20 | 0,8 | 2,0 |
| E | 1,4 | 0,15 | 0,5 | 2,0 |
ცხრილი 10. რეკომენდებული II ტიპის დრეკადი რეაქციის სპექტრის პარამეტრების მნიშვნელობები
| გრუნტის ტიპი | S | TB(s) | Tc(s) | Td(s) |
|---|---|---|---|---|
| A | 1,0 | 0,05 | 0,25 | 1,2 |
| B | 1,35 | 0,05 | 0,25 | 1,2 |
| C | 1,5 | 0,10 | 0,25 | 1,2 |
| D | 1,8 | 0,10 | 0,25 | 1,2 |
| E | 1,6 | 0,05 | 0,30 | 1,2 |
ნახ.24. რეკომენდებული I ტიპის დრეკადი რეაქციის სპექტრი A-E ტიპის გრუნტებისათვის (5%-ანი ჩაქრობისათვის)
ნახ.25.რეკომენდებული II ტიპის დრეკადი რეაქციის სპექტრი A-E ტიპის გრუნტებისათვის (5%-ანი ჩაქრობისათვის)
სეისმური ზემოქმედების ვერტიკალური მდგენელი შეიძლება წარმოდგენილი იქნეს დრეკადი რეაქციის სპექტრის Sv (T)-ს საშუალებით, რომელიც განისაზღვრება ქვემოთ მოყვანილი გამოსახულებებით:
- 0 ≤ T ≤ TB : Sve (T) = avg S [1 + T/ TB (η 3,0– 1)] (30)
- TB≤ T≤ TC : Sve (T) = avg S η 3,0 (31)
- TC ≤ T ≤ TD : Sve (T) = avg S η 3,0 [TC / TD ] (32)
- TD ≤ T ≤ 4s : Sve (T) = avg S η 3,0 [TC TD /T2 ] (33)
ცხრილი 11. ვერტიკალური დრეკადი რეაქციის სპექტრის პარამეტრების რეკომენდებული მნიშვნელობები
| სპექტრი | avg / ag | TB(s) | TC(s) | TD(s) |
|---|---|---|---|---|
| 1 ტიპი | 0,90 | 0,05 | 0,15 | 1,0 |
| 2 ტიპი | 0,45 | 0,05 | 0,15 | 1,0 |
განივი ტალღის საშუალო სიჩქარე, vs, 30 უნდა გამოითვალოს შემდეგი გამოსახულებით:
სადაც hi არის i–ური ფორმაციის ან შრის სისქე მ-ში, ხოლო vi არის განივი ტალღის სიჩქარე (ძვრის დეფორმაციის დონისათვის ≤105) ყველა N შრისათვის 30მ სიღრმემდე. სამშენებლო მოედანი კლასიფიცირებული უნდა იყოს განივი ტალღის გავრცელების საშუალო სიჩქარით, vs,R, თუ ეს შესაძლებელია. სხვა შემთხვევაში გამოყენებული უნდა იყოს NSPT სიდიდე.
გათხევადების ეფექტის გათვალისწინება ფერდობების სეისმური მდგრადობის გაანგარიშებისას
გათხევადების საფრთხის უგულვებელყოფა ფერდობების სეისმური მდგრადობის გაანგარიშებისას შესაძლებელია, როცა აშ<0,15 და კმაყოფილდება სულ მცირე 1 პირობა ქვემოთ მოყვანილი პირობებიდან: /28/
- ქვიშა შეიცავს 20%-ზე მეტ თიხას პლასტიურობის ინდექსით PI>10;
- ქვიშა შეიცავს 35%-ზე მეტ თიხნარს და ამავე დროს SPT–ს დარტყმების რიცხვი ნორმალიზებული ზედაპირული ეფექტისათვის და ენერგიის კოეფიციენტი N1(60) >60;
ცხრილი 12. გრუნტის ტიპები
| გრუნტის ტიპები | სტრატიგრაფიული პროფილის აღწერა | |||
|---|---|---|---|---|
| Vs,30 მ/წმ | Nspt (დარტყმა/30სმ) | Cu (kPa) | ||
| A | კლდე ან კლდის მსგავსი გეოლოგიური ფორმაცია,რომელიც შეიძლება შეიცავდეს არა უმეტეს 5.0 მ-ს სუსტ ზედაპირულ ქანს | >800 | ||
| B | ქვიშის და ხრეშის მკვრივი დანალექები ან ძალიან მკვრივი სულ მცირე რამდენიმე ათეული მეტრი, რომელიც ხასიათდება სიღრმეში თანდათანობით მზარდი მექანიკური მახასიათებლებით | 360 - 800 | >50 | >250 |
| C | მკვრივი ან საშუალო სიმკვრივის სილის, ხრეშის სიღრმისეული დანალექი ან მკვრივი თიხა, რომელთა სისქე რამდენიმე მეტრიდან ასეულ მეტრამდე აღწევს. | 180 -360 | 15 - 50 | 70 - 250 |
| D | ფხვიერიდან საშუალომდე შეჭიდულობის მქონე დანალექი გრუნტები,(რომელიც შეიძლება შეიცავდეს სუსტი შეჭიდულობის შრეებს) ან შრეები, რომლებშიც რბილიდან-საშუალომდე შეჭიდულობის მქონე გრუნტები დომინირებს | <180 | <15 | <70 |
| E | პროფილი, რომლის ზედა შრე სისქით 5-დან 20მ-მდე არის ალუვიუმი, რომელსაც აქვს C და D ტიპის გრუნტისათვის დამახასიათებელი განივი ტალღის გავრცელების Vs სიჩქარე, ხოლო მის ქვემოთ განლაგებულია უფრო მკვრივი გრუნტი, რომლის Vs >800მ/წმ. | |||
| S1 | დანალექი, რომელიც შედგება ან შეიცავს ცულ მცირე 10მ-ის სისქის რბილ თიხა/შლამის (თიხნარის) შრეს მაღალი პლასტიურობის ინდექსით (PI >49) და მაღალი წყალშემცველობით | <100 (მაჩვენებელი) | 0-20 | |
| S2 | დანალექი გათხევადებული გრუნტი, როგორიცაა მგრძნობიარე თიხა ან ნებისმიერი გრუნტის პროფილი, რომელიც არ არის მოყვანილი A-E ან S1-ში |
ქვიშა არის წმინდა, SPT–ს დარტყმების რიცხვით ნორმალიზებული ზედაპირული ეფექტისათვის და ენერგიის კოეფიციენტით N1(60) >30.
თუ გათხევადების საშიშროების უგულვებელყოფა შეუძლებელია, ის განსაზღვრული უნდა იქნეს მინიმუმ საინჟინრო სეისმოლოგიის ცნობილი მეთოდებით, რომლებიც ეფუძნება საველე კვლევების კორელაციას ზედაპირულ გაზომვებსა და კრიტიკულ ციკლურ ძვრის ძაბვებს შორის, თუ ცნობილია, რომ ბოლო მიწისძვრამ ამ ადგილზე გამოიწვია გათხევადება.
ძვრის ძაბვა ასეთ შემთხვევაში შეიძლება განისაზღვროს მარტივი გამოსახულებიდან შემდეგნაირად:
- τ e= 0,65 aS σvo (35)
სადაც σvo არის მთლიანი ზედაპირული დაწნევა, დანარჩენი სიდიდეები განსაზღვრულია ზემოთ. ამ გამოსახულების გამოყენება არ შეიძლება 20მ-ის მეტი სიღრმისათვის.
გათხევადების გამარტივებული ანგარიშისათვის გამოიყენება ემპირიული გრაფიკები. გრაფიკებზე (ნახ.26) ჰორიზონტალურ ღერძზე მოცემულია გრუნტის მახასიათებლები, რაც გამოხატულია ნორმალიზებული პენეტრაციული მედეგობის ან განივი ტალღის გავლის სიჩქარის სიდიდით. ვერტიკალურ ღერძზე მოცემულია ციკლური ძაბვის კოეფიციენტი τe/σ’vo, ანუ მიწისძვრით გამოწვეული ციკლური ძვრის τe ძაბვის შეფარდება ეფექტურ σ’vo, ძაბვასთან. გრაფიკებზე აგებულია ციკლური მედეგობის ზღვრული მრუდი, რომელიც ჰყოფს გაუწყლოვანების (მარჯვნივ) და გათხევადების (მარცხნივ და ზემოთ) შესაძლებლობას. ზოგჯერ ერთზე მეტი მრუდია მოცემული სხვადასხვა სიწმინდის მარცლების შემცველი გრუნტისათვის ან განსხვავებული მაგნიტუდისათვის. ნახ.26-ზე მოცემული გრაფიკები შეესაბამება 7,5 მაგნიტუდის MS-ის მნიშვნელობას, 13 ცხრილში კი მოცემულია მარეგულირებელი კოეფიციენტები, CM სხვადასხვა მაგნიტუდისათვის, რომელთა გადამრავლებით ორდინატაზე, შესაძლებელია ციკლური ძაბვის კოეფიციენტის მნიშვნელობის მიღება შესაბამისი მაგნიტუდისათვის.
ცხრილი13. მარეგულირებელი კოეფიციენტი სხვადასხვა მაგნიტუდისათვის
| Ms | CM |
|---|---|
| 5,5 | 2,86 |
| 6,0 | 2,20 |
| 6,5 | 1,69 |
| 7,0 | 1,30 |
| 9,0 | 0,67 |
როდესაც გათხევადებული ფუძე, სისქით 10სმ, გვხვდება შრეებს შორის, მაშინ ემპირიული გრაფიკების გამოყენებისაგნ უმჯობესია თავის შეკავება.
გათხევადება არ უნდა განვითარდეს τc-ს გარკვეული ზღვარის დაბლა, რადგანაც ფუძე იქცევა როგორც დრეკადი ტანი და არც ფოროვანი დაწნევის აკუმულაცია ხდება.
ნახ26. დამოკიდებულება გათხევადების გამომწვევ ციკლური ძაბვის კოეფიციენტსა, τc/σ’vo და N1(60) –ის სიდიდეს შორის 7,5 მაგნიტუდისათვის სუფთა ქვიშისათვის (A) და სხვადასხვა სიწმინდის თიხნარიანი ქვიშისათვის (B): 1 მრუდი -35% სიწმინდით, 2 მრუდი – 15% სიწმინდით, 3 მრუდი - <5% სიწმინდით.
შენიშვნა: 13 ცხრილში მოყვანილი ციკლური ძაბვის კოეფიციენტის გამოსათვლელი მარეგულირებელი კოეფიციენტის მნიშვნელობები სხვადასხვა მაგნიტუდასათვის (გარდა საბაზო – 7,5 მაგნიტუდისათვის) გაზრდილია 3 ცხრილში მოყვანილ სიდიდეებთან შედარებით. ეს კი გვაძლევს ციკლური ძაბვის კოეფიციენტისა და შესაბამისად ძვრის ძაბვის გაზრდილ მნიშვნელობას.
ტოპოგრაფიული გაძლიერების ფაქტორი
გრუნტის ტოპოგრაფიული გაძლიერების ფაქტორი სეისმური ზემოქმედებისას გამოიყენება პირველი მიახლოებისათვის დამოუკიდებლად რხევის ძირითადი პერიოდისაგან. როგორც მუდმივი მასშტაბური პარამეტრი იგი მრავლდება დრეკადი სპექტრის ორდინატაზე, რომლებიც მოცემულია ნახ.24 და 25-ზე /29/. ამ პარამეტრის გამოყენება უმჯობესია გამოყენებული იყოს ისეთი ფერდობების გაანგარიშებისათვის, რომლებიც მიეკუთვნებიან ორგანზომილებიან ტოპოგრაფიულ არარეგულარობას სიმაღლით 30მ-ზე მეტი. თუ ფერდობის საშუალო დახრის კუთხე ნაკლებია 150-ზე, შესაძლებელია ტოპოგრაფიული ფაქტორის უგულვებელყოფა. წინააღმდეგ შემთხვევაში გასათვალისწინებელია შემდეგი პირობები:
- ცალკე მდგომი ციცაბო კლდისათვის და ფერდობისათვის სიდიდე შთ 1,2 გამოყენებული უნდა იქნეს ფერდობის წვეროსთან ახლო მდებარე ფერდისათვის;
- ქედისთვის წვეროს მნიშვნელოვნად უფრო მცირე სიგანით, ვიდრე ფერდობის ფუძეა, სიდიდე ST 1,4 გამოყენებული უნდა იქნეს ფერდობის წვეროს ახლოს, როცა ფერდობის საშუალო დახრა მეტია 300-ზე და სიდიდე შთ 1,2 გამოყენებული უნდა იქნეს ფერდობის უფრო მცირე დახრისათვის;
- ფხვიერი ზედაპირული ფენის არსებობისას ST-ს სიდიდის უმცირესი მნიშვნელობა სულ მცირე 20%-ით უნდა იყოს გაზრდილი ა) და ბ)-ში მოცემულ სიდიდეებთან შედარებით;
- ST სიდიდე შეიძლება განხილული იქნეს როგორც შემცირებადი წრფივი ფუნქცია ციცაბო კლდისა და ფერდობის მთელ სიმაღლეზე და მისი მნიშვნელობა ერთის ტოლია ფუძესთან.
ზოგადად, სეისმური გაძლიერების ფაქტორი ასევე პირდაპირ მცირდება ქედის სიღრმეში. აქედან გამომდინარე, ტოპოგრაფიული ეფექტები გათვალისწინებული უნდა იყოს მდგრადობის ანგარიშებში, უმეტესად ქედის გასწვრივ მდებარე ზედაპირული თხემის შემთხვევაში და ნაკლებად, როცა მეწყერი ღრმად არის ჩამჯდარი და რღვევის ზედაპირი გადის ფუძის ახლოს. ამ უკანასკნელის შემთხვევაში თუ გამოყენებული იქნება ფსევდო-სტატიკური მეთოდით ანგარიში, შესაძლებელია ტოპოგრაფიული ეფექტის უგულვებელყოფა.
თავი 6 - ფერდობების მდგრადობის გაზრდის ზოგიერთი ღონისძიება
იმ შემთხვევაში, როდესაც გაანგარიშებიდან ჩანს, რომ უსაფრთხოების ფაქტორი საკმაოდ დაბალია, ვიდრე ეს საჭიროა, მაშინ განხორციელებული უნდა იქნეს ისეთი ღონისძიებები, რომლებიც შეძლებენ განსახილველი ფერდობის მდგრადობის გაზრდას საჭირო ზღვრამდე. საერთოდ არ არსებობს ერთიანი ეფექტური ღონისძიებები ყველა ფერდობისათვის და ინჟინერ-დამპროექტებელს უხდება ყოველ ცალკეულ შემთხვევაში მდგომარეობის შესაბამისად მიიღოს გადაწყვეტილება. ფერდობი გაანგარიშების შედეგად თუ მიჩნეულია მდგრადადაც კი, მაინც საჭიროა მისი დაცვა, რათა თავიდან იქნეს აცილებული ატმოსფერული ნალექებისაგან გამოწვეული ძვრის სიმტკიცის დეგრადაცია, ფერდობის ქუსლის ეროზირება და გრუნტში განვითარებული მაღალი წყლის დაწნევისას ფერდობი დარჩეს მდგრადი მზარდი დატვირთვის შემთხვევაშიც.
ყველაზე მარტივად ეს შეიძლება განხორციელდეს შემდეგნაირად:
- საერთოდ ფერდობის დანგრევის რისკის თავიდან აცილებით, რაც იმაში გამოიხატება რომ არასტაბილურ ფერდობზე დაუშვებელი უნდა იყოს რაიმე მშენებლობის დაწყება. გარდა ამისა დადგენილი უნდა იყოს ის მანძილი, რომელიც უზრუნველყოფს ფერდობის დანგრევის შემთხვევაში ფერდობის მახლობლად აშენებული ნაგებობების უსაფრთხოებას. ეს მანძილი უნდა განისაზღვროს ფერდობის კონფიგურაციით, მისი შესაძლო დანგრევის ფორმით, დაცურების ზედაპირის უსაფრთხოების ფაქტორის სიდიდით და დანგრევის პოტენციალური შედეგებით. ამ მანძილის დადგენა ზუსტად არ ხერხდება. აქედან გამომდინარე ამ საკითხის გადაწყვეტა ინჟენერ-გეოლოგის პრეროგატივაა.
- ფერდობის მდგრადობის გასაუმჯობესებლად ფერდობის ზედაპირის ქანების გრანულომეტრიული შემადგენლობის შეცვლით: ზოგ შემთხვევაში შესაძლებელია მთლიანად მოხსნილი იქნეს ფერდობის ზედაპირიდან ისეთი გრუნტი, რომელიც ხელს უწყობს მის არასტაბილურობას და შეცვლილი იქნეს მაღალი სიმტკიცის გრუნტით. ეს ღონისძიება შედეგად იძლევა ფერდობისათვის მოთხოვნილი მინიმალურ უსაფრთხოების ფაქტორის სიდიდეს. გამოსაცვლელი გრუნტი შეიცავს კოლუვიუმს, მეწყერის მიერ ჩამოტანილ ნამსხვრევებს და ნარიყს. ფერდობის გრუნტის გრანულომეტრიული შემადგენლობის შეცვლა ფერდობის მდგრადობის პრობლემის გადასაწყვეტად ზოგჯერ ძალიან ძნელი განსახორციელებელია სხვადასხვა მიზეზის გამო (მაგ. თუ ფერდობი ძალიან დამრეცია და/ან გრუნტი ძალიან დაბალი სიმტკიცისაა). ასეთ შემთხვევაში შესაძლებელია გრუნტის მცურავი მასების მდგრადობის უზრუნველსაყოფად მექანიკური საშუალებების გამოყენება ან გრუნტის გაუმჯობესება მინარევებით, კირთან ან ცემენტთან. თუ გრუნტი 50%-ანი სიწმინდისაა, მისი შერევა ცემენტთან არ ივარგებს, მას უფრო კირთან ურევენ. ფერდობის მდგრადობის გაზრდა შესაძლებელია აგრეთვე ფერდობის დამრეცობის შეცვლით და/ან სიმაღლის დაწევით. ასეთ შემთხვევაში მიზანშეწონილია ფერდობის დრენირებაც. თუ ხელოვნური ფერდობის აგება ხორციელდება სუსტ თიხაზე, მაშინ თიხის მზიდუნარიანობის გაზრდა შეიძლება განხორციელდეს მისი გამკვრივებით ნაგებობის წონით, რომელიც ეტაპობრივად შენდება.
- გაუწყლოვანებით. თუ მიწის ნაგებობის ფუძე წარმოადგენს წყლითგაჯერებულ გრუნტს ან ისეთ გრუნტს, რომელიც შესაძლებელია მომავალში აღმოჩნდეს წყლითგაჯერებული და ამ მიზეზით განვითარდეს მიწის ნაგებობის სიმტკიცის დაკარგვა, ასეთი გრუნტების ხელოვნური გამკვრივება უნდა მოხდეს ეტაპობრივად ვიბროსაგორავებით ან დამტკეპნავი მანქანებით. თუ ფერდობის ტანში ან მის ფუძეში გამოვლენილია მისი არამდგრადობის კავშირი ფოროვან წყალთან, ან წყლის სხვა გავლენასთან, მაშინ საჭიროა ასეთი ფერდობის დრენირება, რისთვისაც იყენებენ ჰორიზონტალურ სადრენაჟო ჭაბურღილებს ან სხვა მსგავს მოწყობილობებს. მიწისქვეშა წყლების დაწნევის შესამცირებლად წარმატებით შეიძლება გამოყენებული იქნეს ვერტიკალური სადრენაჟო ჭაბურღილები და შთანმთქმელი ჭები. როდესაც ხდება ფერდობების სტაბილირება იმ უბნებზე, სადაც შესაძლებელია ტალახის ნაკადების განვითარება. უპირატესობა ეძლევა ისეთ ღონისძიებებს, რომლებიც შეაჩერებს ფერდობის ტანის დამატებით გათხევადებას, თუ მოხერხდება ფერდობის გაცილებით ზემოთ მდებარე უბნებიდან დამეწყრილი ფერდობისაკენ მომდინარე ზედაპირული და მიწისქვეშა წყლების ე.წ. “დაჭერა”, ან თვით ფერდობზე მოეწყობა ისეთი საფარი, რომელიც შეაჩერებს წყლის ინფილტრაციას ზედაპირიდან ფერდობის ტანში, რათა არ მოხდეს ფერდობის ფუძის ძვრისადმი სიმტკიცისა და მედეგობის შემცირება ტივტივის ეფექტის გამო და შედეგად ფერდობის დაცურება-დანგრევა. /31,32,33,/
- თვით ფერდობის გამაგრება-გაძლიერებით: თუ ზემოთ მოყვანილი ღონისძიებები საკმარისი არ აღმოჩნდა, მაშინ საჭიროა გამოყენებული იქნეს ფერდობის მდგრადობის გასაზრდელად მექანიკური საშუალებები, როგორიცაა: საყრდენი კედლები, ღრმა დასაძირკვლება (მაგ. ხიმინჯები ან ნაბურღი ღეროები), ფუძის გამაგრება გეოსინთეტიკით, საჭიმარიანი ანკერებით ან გრუნტის მანჭვალებით.
საყრდენი კონსტრუქციების ტიპები მოყვანილია ნახ.27-ზე. /30/
ნახ.27. საყრდენი კონსტრუქციების ტიპები.
- გრავიტაციული კედელი _ ქვის, ბეტონის,კონსოლიანი ან ძელყორე;
- საჭიმარიანი ან გრუნტის მანჭვალიანი კედლები;
- შპუნტიან-ხიმინჯიანი ან ხიმინჯების მწკრივიანი და ხის შემოფიცვრიანი კედლები;
- გეოსინთეტიკით ან გეოგრიდით დაარმატურებული კედლები.
საყრდენი კედლის დაკონსტრუირება ხდება ისე, რომ უზრუნველყოფილი იყოს არამდგრადი ფერდობების დამატებითი მედეგობა და უსაფრთხოების ფაქტორის გაზრდა კედლის უკან მოთავსებული გრუნტისათვის საჭირო დონემდე. საყრდენი კონსტრუქცია უნდა მოთავსდეს შესაძლო დაცურების ან გადაყირავების ადგილზე.
ფერდობების უსაფრთხოების ფაქტორის გაზრდა შესაძლებელია ხიმინჯების მწკრივის/ნაბურღი ღეროების ჩამაგრებით, რომლებიც წვერით დაეყრდნობიან მდგრად გრუნტებს, რაც გაზრდის ფერდობის მდგრადობას ჰორიზონტალური მიმართულებით გადაადგილების შემცირებით. /34/
საჭიმარიანი ანკერების გამოყენება შესაძლებელია ხიმინჯების მწკრივის/ნაბურღი ღეროების გარეშეც, აგრეთვე იმ შემთხვევაშიც, თუ საჭიროა დამატებითი მედეგობის განვითარება. საჭიმარიანი ანკერები კეთდება ფოლადის ღეროებისაგან ან კაბელებისაგან, რომლებიც შედგომ ჩამაგრდება გაბურღულ, დახრილ შახტაში. ანკერები ჩამაგრების შემდეგ იჭიმება მანამდე, ვიდრე შახტაში ჩასხმული თხელი სამშენებლო ხსნარი არ მიაღწევს საანგარიშო სიმტკიცეს. ანკერებს ცდიან საანგარიშოზე მეტ დატვირთვაზე. დროებითი ანკერების დაცვა კოროზიისაგან არ არის საჭირო, მაშინ, როდესაც მუდმივი ანკერები კოროზიისაგან აუცილებლად დაცული უნდა იყოს.
გრუნტის მანჭვალი წარმოადგენს დაუძაბავ ღეროს, რომელიც იბურღება ფერდობის ტანში და ნახვრეტი ივსება ბეტონით. მას არ იყენებენ შედარებით წმინდა ღორღისა და ქვიშიანი ფუძის შემთხვევაში ფერდობის მუდმივი სტაბილიზაციისათვის და მას დროებითი დანიშნულება აქვს თიხნარიანი ფერდობის გასამაგრებლად.
ნაყარიანი ფერდობის საყრდენად შეიძლება გამოყენებული იქნეს აგრეთვე ანაკრები ბეტონის ძელყორე კედელი (ნახ. 28) /36/
ნახ 28. ანაკრები ბეტონის ძელყორე კედელი ფერდობის შესაკავებლად
საქართველოშიც, როგორც მთაგორიან ქვეყანაში, მეწყერები ფართოდაა გავრცელებული. ჩვენი ტერიტორიის დიდი ნაწილის და მათ შორის თბილისის ძირითადი ქანები წარმოადგენილია თიხაფიქალების ან არგილიტების შუაშრეებიანი ქვიშაქვებით, რომლებიც მაშინ წარმოიშვა, როდესაც კავკასია ზღვის ფსკერი იყო. ეს ქანები დაფენილია არა ჰორიზონტალურად, არამედ დახრილად საკმაოდ დიდი დახრის კუთხით.
შენობის ქვაბულის ან კომუნიკაციების თხრილების დამუშავებისას ან გარაჟების მოწყობის მიზნით ხდება კლდის დახრილი ფენების წაკვეთა, რაც იწვევს გრუნტის მასის ჩამოქცევის საშიშროებას. ასეთ შემთხვევაში კლდის მასების შესაკავებლად კეთდება რკინაბეტონის კონტრფორსები, რომლებიც მიბჯენილია კლდეში მოწყობილ ჩაღრმავებაზე. ამავე დროს კლდის მასივში შეჭრა არ უნდა იყოს დიდი და გრუნტი უნდა დამუშავდეს მექანიკურად.
განსაკუთრებით ხშირად დამეწყრილი ტერიტორიის გვერდის ავლის ან მასზე გავლის პრობლემა დგას რკინიგზებისა და საავტომობილო გზების გაყვანისას – ხდება ხეობაში გამავალი გზის მოცილება დამეწყრილი ადგილიდან მისი გადატანით მდინარის მეორე ნაპირზე - გვირაბებისა და ესტაკადების მოწყობით. ამ მიზნით საქართველოს ტერიტორიის შავი ზღვის პირას გამავალი რკინიგზის ნაწილი გვირაბშია შეტანილი.
საქართველოში დაინგრა და დაზიანდა რამდენიმე სამრეწველო ნაგებობა და კაპიტალური შენობა, რომელიც აგებული იყო მეწყერზე ან მეწყერის მოქმედების ზონაში _ ქ. მარნეულის კომბინატის საწყობები, ქ. ჭიათურის გამამდიდრებელი ფაბრიკა, რაჭის თეთრი დარიშხანის სამრეწველო კომპლექსის ზოგიერთი შენობა და სხვა.
რაჭის თეთრი დარიშხანის სამრეწველო კომპლექსის მოედნის ნაწილი მოხვდა მძლავრი მეწყერის ფარგლებში. გატარებული ღონისძიებებით მოწესრიგდა ზედაპირული წყლების დინება და დინება გაყვანილი იქნა მეწყერის ფარგლებიდან. ამავე დროს მეწყერის ზედა ნაწილში, სადაც მისი სიმძლავრე შედარებით მცირე იყო, მოეწყო დრენაჟი.
ქ.თბილისში, ბარალეთის ქუჩაზე, მრავალსართულიანი შენობა, სკოლა, საწარმოო დანიშნულების ნაგბობები აშენდა მეწყერის ენის სიახლოვეს. მეწყერის ფარგლებში გაყვანილი წყალსადენის მილის გახეთქვამ გამოიწვია გრუნტის დასველება, ნაწილობრივ გაჯირჯვა და ჩამოწოლა, რასაც თავის მხრივ მოჰყვა მეწყერის გააქტიურება და საფრთხე შეექმნა მასთან ახლოს მდებარე ნაგებობებს. მეწყერის შემდგომი მოძრაობის შესაკავებლად განხორციელდა 1,5მ დიამეტრის მქონე ნაბურღ-ნატენი რკინაბეტონის ხიმინჯებისაგან შემდგარი ნაგებობა, რომელიც ზემოდან გაერთიანდა რკინაბეტონის როსტვერკით.
ქ. თბილისში, მდ. ხევძმარის ერთერთ არამდგრად ფერდზე აგებული შენობის ყველა წყალშემცველი კომუნიკაცია ამოტანილი იქნა მიწის ზედაპირზე, რათა დაზიანების შემთხვევაში მათი შემჩნევა შესაძლებელი გამხდარიყო, გარდა ამისა თვით მდინარე მოთავსდა მილში და ხევი შეივსო გრუნტით, რამაც შეამცირა მეწყერის, როგორც მთლიანი მასის მოძრაობა.
მცირე სიდიდის მეწყერისა და სუსტი ადგილების დასამაგრებლად საუკეთესო საშუალებაა მცენარეების დარგვა, მაგ. აკაციების. ითვლება, რომ აკაციების ღრმა ფესვებმა მნიშვნელოვანი როლი შეასრულა იმ ბორცვის მდგრადობის შენარჩუნებაში, რომელზეც დგას თბილისის ცირკის შენობა, რადგანაც ბორცვი შედგება გათხევადებული პლასტიკური მდგომარეობაში მყოფი ფენებისაგან.
მეწყერის სტაბილიზაციისაკენ მიმართული ღონისძიებები და განსაკუთრებით კი მისი შემკავებელი ნაგებობების მშენებლობა და ექსპლოატაცია დაკავშირებულია მნიშვნელოვან და შრომატევად სამუშაოებთან. ამიტომ მიზანშეწონილი იქნება, თუ კაპიტალური შენობა-ნაგებობები, ყველა შემთხვევაში, აიგება მდგრად მოედნებზე. /39/
თავი 7 - გრუნტის მათემატიკური მოდელების განვითარება და გამოყენება
მიწის ფერდობების სეისმომედეგობაზე გაანგარიშებისას დაცული უნდა იყოს 2 პირობა: აცილებული უნდა იყოს სეისმური არამდგრადობა და დიდი დეფორმაციების (გადაადგილებების, ჯდენების და ბზარების) განვითარება, ამისთვის კი შეფასებული უნდა იქნეს გრუნტის მასალის სიმტკიცის მახასიათებლები. დაძაბულ-დეფორმირებული მდგომარეობა კი უნდა განისაზღვროს გრუნტის მასალისათვის დამახასიათებელი ძაბვებისა და დეფორმაციების არაწრფივი დამოკიდებულების მხედველობაში მიღებით. როგორც წესი, ეს ხორციელდება პლასტიკური დეფორმაციის თეორიაზე ან პლასტიკური დენადობის თეორიაზე დაყრდნობით, რასაც რთული ექსპერიმენტული (სამღერძა) კვლევების ჩატარება სჭირდება. (რეტროსპექტული გაანგარიშებისას, როცა არ არსებობს შესაბამისი კვლევები, შესაძლებელია გამოყენებული იქნეს არსებული გეოლოგიური მონაცემები. ასეთ შემთხვევაში აუცილებელია ისეთი მათემატიკური მოდელების შექმნა, რომელიც დაეფუძნება ერთღერძა ექსპერიმენტულ მონაცემებს, მაგრამ გამოსაყენებელი იქნება დეფორმაციებსა და ძაბვებს შორის არაწრფივი დამოკიდებულების გამოსახატავად).
გრუნტის დრეკად-პლასტიკური მოდელები წარმოადგენენ გეოლოგიური მასალის ისეთ კლასს, რომლებსაც შეუძლიათ რაღაც ხარისხით როგორც ფიზიკური რეალობის, ასევე პოტენციურად საიმედო რიცხვითი შედეგების მოცემა და მათი ერთერთი უპირატესობა იმაშიც მდგომარეობს, რომ თეორიები, რომლებსაც ისინი ეყრდნობიან, კარგად არის განვითარებული და მათ წინ უსწრებდათ ლითონის პლასტიკურობის თეორიის განვითარება. პლასტიკური დეფორმაციის თეორიის ჩარჩოებში ანგარიში ტარდება ისეთი მოდელების გამოყენებით, რომლებიც დამოკიდებულია აქტიური დატვირთვისას მიღებული ძაბვების დონეზე, ხოლო განტვირთვისას _ დრეკადობის მოდულებზე.
პირველი, ვინც ლითონის პლასტიკურობის თეორიის გამოყენება სცადა გრუნტის პლასტიკურობისათვის, იყვნენ დრაკერი და პრეგერი, როცა ისინი აფართოებდნენ ფონ მიზესის დენადობის კრიტერიუმს გრანულირებული სივრცისათვის შეზღუდული განმტკიცების გათვალისწინებით. შედეგად მიიღეს დენადობის ახალი კრიტერიუმი, რასაც ახლა დრაკერ-პრეგერის კრიტერიუმი ჰქვია. შემდგომში მათ ჩათვალეს, რომ გრუნტის სივრცული პლასტიკური ქცევა წარმატებულად შეიძლება მოდელირებული იქნეს დეფორმაციის გამამტკიცებელი კუმშვის კაპ ზედაპირით, რომელიც არ ხურავს დრაკერ-პრეგერის დანგრევის მოხაზულობის ღია ბოლოს. გრუნტის წინამორბედი მოდელი და დენადობის კრიტერიუმი კი, როგორიცაა მორ-კულონის, ითვალისწინებდა ხახუნის შეზღუდულ ქცევას. /41/.
გარე ფაქტორების გავლენით გრუნტების პლასტიკური დეფორმაცია იგვიანებს დროში დაძაბულ მდგომარეობასთან მიმართებაში. გრუნტში ამ დროს ვითარდება ბლანტპლასტიკური დეფორმაციები. დაგვიანების დრო მუდმივი არ არის და დამოკიდებულია როგორც გრუნტის თვისებებზე, ასევე ზემოქმედების სიდიდეზე და ხასიათზე. მაგ. როცა დაძაბული მდგომარეობა უახლოვდება ზღვრულს, მაშინ დეფორმაციის სტაბილიზაციის პერიოდი დიდდება
კოიტერის განმამტკიცებელი პლასტიკური გარემოს განზოგადებული ასოცირებული დენადობის კანონი ეფუძნება ძაბვების რეალური სივრცისათვის ენერგიის დისიპაციის მაქსიმუმის პრინციპს და ამავე დროს თავისთავში მოიცავს, როგორც კერძო შემთხვევას, დაცურების თეორიას, უშვებს რა დატვირთვის სინგულარული ზედაპირის არსებობას. თუ ხისტპლასტიკურ სისტემაზე მოქმედებს Qi გარე ძალების n სისტემა, მაშინ ზღვრული მდგომარეობის მიღწევის პირობა მოცემული იქნება ასე: F(Q1, Q2, ...,Qn) =0, რითიც ისაზღვრება n განზომილებიან ძალთა სივრცეში დენადობის ზედაპირი Qi. ძალთა მოდების წერტილები დენადობის პირობის მიღწევისას იღებენ qi, სიჩქარეს, რომლის სიდიდე განიხილება როგორც n განზომილებიან სივრცეში ვექტორის მდგენელი, რომლის სიდიდე უცნობია, მაგრამ მას აქვს დენადობის ზედაპირის მიმართ ნორმალის მიმართულება. თვით ძალთა ერთობლიობა, რომლებიც მოქმედებს სისტემაზე, გამოისახება Q ვექტორით. წესს, რომელიც ადგენს სიჩქარეების განაწილებას დენადობის დადგომისას, ჰქვია დენადობის კანონი და ჩაიწერება ასე: qi = λfi(Qk), i,k=1,2,...,n. აქ λ ლაგრანჟის ნებისმიერი დადებითი მამრავლია. თუ F(Q1, Q2, ...,Qn)< 0, დენადობა არ არსებობს და qi = 0. ძალთა სივრცეში გარე დატვირთვის ყოველი კომბინაცია გამოსახულია წერტილით, რომელსაც გააჩნია Qi კოორდინატები. თუ წერტილი მოქცეულია დენადობის ზედაპირის შიგნით, სისტემა ხისტია; თუ წერტილი მდებარეობს ზედაპირზე, ვითარდება დენადობა. დენადობის მდგომარეობა მიიღწევა იმის შედეგად, რომ სისტემის ნაწილების საკმაო რიცხვი გადადის პლასტიკურ მდგომარეობაში. ძალების მოდების წერტილების qi სიჩქარეები გამოითვლება შემდეგნაირად: qi = λ F/ Qi. ამ თანაფარდობას ჰქვია დენადობის ასოცირებული კანონი, რომლის აზრი ის არის, რომ დენადობის კანონი მჭიდროდ არის დაკავშირებული დენადობის პირობასთან, ანუ ის ასოცირებულია ამ პირობასთან /48/. ამ შემთხვევაში დრეკადი დეფორმაციის არის ზღვარი ემთხვევა დატვირთვის ზედაპირს, რომელსაც გააჩნია რეგულარული უბნები და განსაკუთრებული (სინგულარული) წერტილები. ფიზიკური არსი არისა ძაბვების სივრცეში, რომელიც შემოსაზღვრულია დატვირთვის ზედაპირით, არის ის, რომ ამ არის საზღვრებში გრუნტი იქცევა როგორც დრეკადი. დატვირთვებისას, რომლებიც ამ არის გარეთ გამოდის, ვითარდება შეუქცევადი პლასტიკური ძვრისა და მოცულობის დეფორმაციები.
ტერმინი „იდეალური“ პლასტიკურობა იმ აზრით იხმარება, რომ მასალას არ გააჩნია განმტკიცების უნარი და როცა σ=στ, მასალას შეუძლია განუსაზღვრელად დეფორმირება. განმამტკიცებელი პლასტიკური გარემოს დენადობის თეორია ემყარება პრინციპულად იმავე თანაფარდობას, რაზეც ბლანტპლასტიკური გარემოს დენადობის თეორია. განსხვავება მდგომარეობს მხოლოდ იმაში, რომ დატვირთვის ფუნქცია დამოკიდებულია პარამეტრზე, რომელსაც განმტკიცების პარამეტრი ჰქვია. ასეთ პარამეტრად შეიძლება მიჩნეული იქნეს პლასტიკური დეფორმაცია და ამგვარად ზღვრულის წინარე მდგომარეობაში დატვირთვის განვითარებული ზედაპირი განსაზღვრავს პლასტიკური დეფორმაციის ვექტორის ნაზრდის სიდიდესა და მიმართულებას. ნარჩენი დეფორმაციების არსებობა გრუნტში წინასწარ განსაზღვრავს დატვირთვის ზედაპირის ჩაკეტილ ფორმას. გრუნტის დილატანსიის ასახვა შესაძლებელია დატვირთვის ფუნქციის ფორმულირებით. დილატანსია წარმოადეგენს გრუნტებისათვის არსებით ფაქტორს და ის შეიძლება იყოს ორი ნიშნის: ძვრის დროს გრუნტი ან გამკვრივდება (კონტრაქცია) ან თანდათან კარგავს სიმკვრივეს. ნიშანი და სიდიდე მოცულობითი დეფორმაციის დილატანსიური ნაწილისა დამოკიდებულია: გრუნტის სიმკვრივეზე, სიმტკიცის ზღვართან მიახლოებულ მდგომარეობის ხარისხზე, დატვირთვის ტრაექტორიაზე, გრუნტის თიხოვნობაზე და სხვა. გრუნტის პლასტიკური დეფორმაციების განვითარება ზღვრულის წინარე მდგომარეობაში შესაძლებელია გათვალისწინებული იქნეს დატვირთვის ზედაპირის ფორმისა და ადგილმდებარეობის დამოკიდებულებით მოცულობითი პლასტიკური დეფორმაციის დაგროვებასა და ფორმის შეცვლის დეფორმაციაზე. ჰიდროსტატიკური შეკუმშვის შედეგად წარმოქმნილი დრეკადი დეფორმაციების არე ფიქსირდება საწყისი დატვირთვის ზედაპირის შეყვანით. პლასტიკური დეფორმაციების ნაზრდის ვექტორის მიმართულების დამოკიდებულება დამატებითი დატვირთვის ვექტორის მიმართულებაზე შეიძლება გათვალისწინებული იქნეს ძალიან მარტივად, თუ დატვირთვის ზედაპირს გააჩნია განსაკუთრებული სინგულარული წერტილები. /42/
მათემატიკური მოდელი გამოიყენება უკვე 20 წელიწადზე მეტია გეოლოგიური მასალის ფართო სპექტრის რეაქციის მოდელირებისათვის. გრუნტის მოდელი პირველად აღწერილი იყო ლიტერატურაში დიმაჯიოსა და სანდლერის მიერ (1971) /43/. სანდლერი თვლიდა, რომ მოცულობითი ჰისტერეზისის წინასწარმეტყველება, რომელსაც ამჟღავნებს უმეტესი გეოლოგიური მასალებისა, შესაძლებელია აღწერილი იქნეს პლასტიკური მოდელით, თუ ეს მოდელი დაფუძნებულია განმამტკიცებელ დენადობის ზედაპირზე, რომელიც შეიცავს ჰიდროსტატიკურ ძაბვის პირობას. მოდელს აქვს სხვა მოსალოდნელი თვისებაც _ უპირველესი მნიშვნელობა აქვს იმას, რომ მას შეუძლია მოცულობითი ჰისტერეზისის გამოვლენა დეფორმაცია-განმტკიცების დენადობის ზედაპირის ან კაპის გამოყენებით. კაპის მოდელირება შესაძლებელია არაწრფივი დანგრევის ზედაპირით, წრფივი ან არაწრფივი დრეკადი მოდულით, ან როგორც ძაბვის მესამე ინვარიანტის ფუნქცია. მასალის პარამეტრების შესაბამისი შერჩევით შესაძლებელია გამოყენებული იყოს დრეკადი ან წრფივი დრეკადი-სრულად პლასტიკური მასალის მოდელი.
პირველადი მოდელების მოდიფიკაციები გაკეთებულია სხვადასხვა მკვლევარების მიერ და ფართოდ გამოიყენება კომპიუტერულ პროგრამებში.
დრაკერ-პრეგერის მოდელი დაფუძნებულია დრაკერ-პრეგერის დენადობის პირობებზე, დრაკერ-პრეგერის და კაპის დენადობის ფუნქციების გამოყენებით დენადობის ასოცირებულ წესზე, სრულიად პლასტიკურ დრაკერ-პრეგერის ქცევაზე, გაჭიმვის ჩამონაჭერზე და კაპის განმამტკიცებელზე. დრაკერის პოსტულატების დაკმაყოფილება უზრუნველყოფს ანგარიშების ერთადერთობას, უწყვეტობას და მდგრადობას და იძლევა სწორად ფორმულირებულ მათემატიკურ პრობლემას. დრაკერის პირველი პოსტულატი იძლევა ისეთ მოდელს, რომელშიც არ განხორციელდება დეფორმაცია- დარბილება. მეორე პირობა შეიცავს ორ მოსაზრებას: პირველი _ დატვირთვის ფუნქცია ან დენადობის ზედაპირი უნდა იყოს ამობურცული და მეორე _ პლასტიკური დეფორმაციის ნაზრდის ვექტორი უნდა იყოს დენადობის ზედაპირის მიმართ ორთოგონალური, რაც იმას ნიშნავს, რომ გამოყენებული უნდა იყოს ასოცირებული დენადობის წესი. დიმაჯიომ და სანდლერმა დაამუშავეს დრეკად-პლასტიკური დრაკერ-პრეგერის კუმშვის განმამტკიცებელი კაპ ზედაპირიანი მოდელი და ჩაატარეს რიცხვითი ანგარიშები (ნახ. 29) /41/
ნახ.29. არაერთგვაროვანი, სამზედაპირიანი, ორი ინვარიანტიანი დრაკერ-პრეგერის კაპ მოდელი ორი კუთხის უბნით
რადგანაც მოდელი აშკარად შეიძლება გამოყენებული ყოფილიყო სასრულო სხვაობებისა და/სასრულო ელემენტების გამოთვლებში, ანგარიშებში დაშვებული იქნა დეფორმაციის ექსტრემალურად მცირე ნაზრდი და არ განიხილებოდა მასალის მხები სიხისტის ოპერატორები. რადგანაც ასეთი კაპ მოდელი პირველად დამუშავებული იყო ქვიშისათვის, ის წარმატებით გამოიყენებოდა აგრეთვე სხვა მასალისთვისაც, როგორიცაა თიხა და ბეტონი. ეს მოდელი ეფუძნებოდა კლასიკურ დრეკად-პლასტიკურ თეორიას და შეწყვილებულ - დრაკერ-პრეგერის რღვევის მოხაზულობას და განმამტკიცებელ კუმშვის კაპ ზედაპირს. მას შემდეგ, რაც ისინი გამოიყენებოდა მასთან დაკავშირებულ დენადობის წესებთან ერთად, შესაძლებელი იყო დილატანსიის დაშვება (სიმტკიცის გაზრდის ეფექტი) (რაც არის პლასტიკური მოცულობის ნაზრდის ზრდა ძვრის დატვირთვის შედეგად). როცა დატვირთვა მოდებულია კუმშვის კაპ ზედაპირზე,ხდება პლასტიკური განმტკიცება (პლასტიკური მოცულობის ნაზრდის შემცირება). დიმაჯიოსა და სანდლერის დამუშავებულ კაპ მოდელებში, განმამტკიცებელი კაპი არის ელიფსური ზედაპირი უდიდესი და უმცირესი რადიუსების მუდმივი შეფარდებით და ის კვეთს ჩამონგრევის მრუდს არაერთგვაროვანი ფორმით. კუმშვის კაპ ზედაპირი განფენილია I1 ღერძის გასწვრივ პლასტიკური მოცულობით დეფორმაციის ნაზრდში ცვლილებით. დილატანსიის გამო კუმშვის კაპი მიმართულია შიგნით, როცა იკუმშება და ის გამოდის გარეთ როცა ფართოვდება პლასტიკური განმტკიცების შემთხვევაში. გადაკვეთის წერტილი ან კუთხის წერტილი, რომელშიც დრაკერ-პრეგერის მრუდი და მოძრავი კუმშვის კაპი იკვეთება, დიდხანს განიხილებოდა როგორც წერტილი, რომელსაც შეეძლო მოეცა ორივე – რიცხვითი და მყარი არასტაბილურობის გაზრდა. ერთერთი წინააღმდეგობა ამ ფაქტიდან ის არის, რომ საწყისი განმტკიცების წესი ასეთი კაპ მოდელებისა წარმოადგენილია ისეთი ფორმით, რაც იძლევა შესაბამისობას კაპ განმტკიცების k პარამეტრსა და პლასტიკურ მოცულობით დეფორმაციას, შორის.
აქედან გამომდინარე, თუ ასეთი განმამტკიცებელი კანონია ფაქტიურად გამოყენებული, მაშინ განვითარდება მოულოდნელი და არასასურველი დამარბილებელი ქცევა, როცა ძაბვის წერტილი არის კუმშვის კუთხის წერტილში. სასურველი კონტროლისა და არასასურველი დამარბილებელი ქცევის თავიდან ასაცილებლად კუმშვის კუთხის წერტილში, სანდლერმა და რუბინმა შესთავაზეს მოდიფიცირებული წყვეტილი გამამყარებელი წესი, რომელიც პრევენციას უკეთებს მასალის დამარბილებელ რეაქციას. რეზენდე და მარტინმა აჩვენეს შესაბამისად, რომ წყვეტილმა განმამტკიცებელმა წესმა შეიძლება მიიყვანოს არასრულყოფილ მოდელამდე იმ აზრით, რომ მას ექნება დეფორმაციის დიაპაზონის სივრცეში კუმშვის სინგულარულ კუთხის წერტილზე უბანი, რომელიც არ შეიძლება დაიფაროს სხვა შესაძლო ძაბვის სივრცით. ძირითადი მიზეზი ასეთი არასრულყოფისა დევს განმამტკიცებელი წესის წყვეტაში კუმშვის კუთხეში.
გამოიყენა რა ელეგანტური ინტეგრირების თეორია არაერთგვაროვანი მრავალზედაპირიანი პლასტიკურობისათვის, სიმომ და სხვ. განავითარეს ძლიერი რიცხვითი კაპ მოდელი დენადობის აქტიურობის ალგორითმის საანგარიშოდ. როგორც ნაწილი მათი ახალი გაანგარიშებისა, სიმომ და სხვ. შესთავაზეს მოდიფიცირებული უწყვეტი განმამტკიცებელი წესი, რომელიც თავიდან აიცილებს დარბილებას და გვერდს აუვლის მთლიანი შედეგების ზრდას. რეზენდესა და მარტინის მიხედვით მათ ჩამოაყალიბეს თანამიმდევრული ალგორითმული დატვირთვა/განტვირთვის პირობები. შემდგომ ჰოფშტეტერმა, სიმომ და ტეილორმა განაახლეს კაპ მოდელის განმამტკიცებელი წესი ისე, რომ შედეგად მიღებული იქნა სიმეტრიული მდგრადი მხები ოპერატორები. მიუხედავად იმისა, რომ მოხდა არსებითი გაუმჯობესება, პრობლემები დარჩა არამდოვრე სამზედაპირიანი კაპ მოდელის შემთხვევაში. უპირველესი სიძნელე მდგომარეობს იმაში, რომ მასალის მხები ოპერატორები ორივე – კუმშვის კუთხისა და გაჭიმვის კუთხის უბნებში არიან სინგულარული და ამიტომ ისინი ვერ უზრუნველყოფენ მასალის მოცულობით სიხისტეს, რაც მთლიანად არარეალისტურია და მას შეუძლია მიიყვანოს გრუნტის სისტემების კონსტრუქციულ გაანგარიშებებში სიძნელეებამდე. /41/
კაპ მოდელი ფორმულირებულია ძაბვის ტენზორის ინვარიანტის გამოსახულებებით. კვადრატული ფესვი დევიატორული ტენზორის მეორე ინვარიანტიდან შეიძლება მოიძებნოს დევიატორული ძაბვებიდან შემდეგნაირად:
ეს არის ობიექტური სკალარული საზომი დეფორმაციისა ან ძვრის ძაბვისა. პირველი ინვარიანტი I1 ძაბვისა არის ძაბვის ტენზორის კვალი.
ყველაზე დიდი უპირატესობა ამ კაპ მოდელისა სხვა დანარჩენ კლასიკურ დაწნევაზე დამოკიდებულ პლასტიკურ მოდელებთან შედარებით არის შესაძლებლობა ძვრის დატვირთვისაგან განვითარებული დილატანსიის სიდიდის კონტროლისა. დილატანსია ვითარდება ძვრის დატვირთვისას როგორც შედეგი დენადობის ზედაპირისა, რომელსაც აქვს დადებითი მიმართულების დახრა √ID– I სივრცეში. ასე რომ პლასტიკური დენადობის განსაზღვრა იმ მიმართულებით, რომელსაც ექნება დენადობის ზედაპირის მიმართ ნორმალის მიმართულება, წარმოქმნის პლასტიკური დეფორმაციის ვექტორის სიდიდეს, რომელსაც გააჩნია მდგენელი მოცულობითი (ჰიდროსტატიკური) მიმართულებით. მოდელებში, როგორიცაა დრაკერ-პრეგერის და მორ-კულონის, ეს დილატანსია გრძელდება ისე დიდხანს, სანამ ძვრის დატვირთვაა მოდებული და ბევრ შემთხვევაში იწვევს გაცილებით მეტ დილატანსიას, ვიდრე ეს აღინიშნება ექსპერიმენტებში. კაპ მოდელში, როდესაც დანგრევის ზედაპირი აქტიურია, დილატანსია ვითარდება ისევე, როგორც დრაკერ-პრეგერის და მორ-კულონის მოდელებში. მაგრამ განმტკიცების კანონი უშვებს კაპ ზედაპირის კუმშვას მანამდე, ვიდრე კაპი გადაკვეთს ჩამონგრევის მრუდს ძაბვის წერტილში დენადობის ზედაპირის ლოკალური ნორმალი ახლა ვერტიკალურია და ამიტომ შემდგომი პლასტიკური მოცულობითი დეფორმაცია (დილატანსია) არ წარმოიქმნება. მეორე უპირატესობა ამ კაპ მოდელისა არის შესაძლებლობა მოდელის პლასტიკური შემჭიდროებისა. ამ მოდელში ყველა მცირე მოცულობითი რეაქცია არის დრეკადი მანამდე, ვიდრე ძაბვის წერტილი არ მოხვდება კაპის ზედაპირზე.
სასრულო ელემენტების წესების JAM-ში გამოყენებული კაპ მოდელი. ამ შემთხვევაში დრეკადი მოცულობითი მოდული ისაზღვრება შემდეგნაირად: /43/
სადაც K არის საწყისი დრეკადი მოცულობითი მოდული;
k1 და k2 არის მასალის მუდმივები.
დრეკადი მოცულობითი მოდული იძლევა განტვირთვის მოდულს დაწნევა-მოცულობის სივრცეში.
მასალის სამი მუდმივა შეიძლება განისაზღვროს განტვირთვის მონაცემებიდან, რომლებიც მიიღება ჰიდროსტატიკური დატვირთვის ტესტის განმავლობაში. წარმოდგენილ მოდელში (ნახ.30) დატვირთვის f ფუნქციის დანგრევის მრუდის ნაწილი განსაზღვრულია მოდიფიცირებული დრაკერ-პრეგერის დანგრევის ზედაპირიდან შემდეგი ფორმით:
სადაც A, B და C არის მასალის მუდმივები. დეფორმაციის განმამტკიცებელი დენადობის ზედაპირი ან კაპი აღწერილია შემდეგნაირად:
k არის განმამტკიცებელი პარამეტრი, რომელიც ტოლია პლასტიკური მოცულობითი დეფორმაციისა;
ნახ.30. სასრულო ელემენტების წესების JAM-ში გამოყენებული კაპ მოდელი
მოდიფიცირებული დრაკერ-პრეგერის კაპ მოდელი. დრაკერ-პრეგერის კაპ მოდელი, რომელიც ჩადებულია ABAQUS-1998-ში /46/, წარმოადგენს მასალის ქცევას პერმანენტული დეფორმაციის განმავლობაში. ნახ.31-ზე მოცემულია დენადობის ზედაპირი, აღწერილი კაპ მოდელით p-q (ჰიდროსტატიკური დაწნევა-დევიატორული ძაბვა) სიბრტყეში.
მოდელი ხასიათდება 3 პრინციპული სეგმენტით: დაწნევაზე დამოკიდებული დრაკერ-პრეგერის ძვრის დანგრევის სეგმენტით Fs, კუმშვის კაპით Fc და გადასვლის ზედაპირით Ft. მოცულობითი დეფორმაციის გამყარება განსაზღვრულია კაპის მოძრაობით ჰიდროსტატიკური ღერძის გასწვრივ. მოდელს აქვს 2 დანიშნულება: დააკავშიროს დენადობის ზედაპირი ჰოდროსტატიკურ კუმშვაში, რომელიც ამგვარად ითვალისწინებს არადრეკადი განმტკიცების მექანიზმს, პლასტიკურ კუმშვასთან და გააკონტროლოს მოცულობითი დილატანსია, როცა მასალაში იწყება დენადობა ძვრის დარბილების კანონის გათვალისწინებით, როგორც ისეთ მასალაში, რომელიც ინგრევა დრაკერ-პრეგერის ძვრის დანგრევის ზედაპირზე.
დანგრევის ზედაპირი მერიდიანულ (p-t) სიბრტყეში აღწერილია ძვრის დანგრევის ზედაპირით:
კაპის დანგრევის ზედაპირი:
ნახ.31. დენადობის ზედაპირი, განსაზღვრული მოდიფიცირებული დრაკერ-პრეგერის კაპ მოდელით
და გადასვლის დანგრევის ზედაპირი:
სადაც β არის ხახუნის კუთხე, d არის მასალის შეჭიდულობა, t არის დევიატორული ძაბვის საზომი, p არის ექვივალენტური დაწნევის ძაბვა, R არის ელიფსური კაპის ჰორიზონტალური ღერძის შეფარდება ელიფსური კაპის ვერტიკალურ ღერძთან, pa(εplvol) წარმოადგენს მოცულობით არადრეკად-დეფორმაცია-წამყვან განმტკიცებას და/ან დარბილებას და α არის გადასვლის ზედაპირის რადიუსის შეფარდება (p-t) სიბრტყეში ელიფსური კაპის ვერტიკალური ღერძის რადიუსთან.
განმამტკიცებელი/დამარბილებელი კანონი განსაზღვრულია უბან-უბან წრფივი ფუნქციით ჰიდროსტატიკური კუმშვის დენადობის ძაბვის პბ-ს დამოკიდებულებით მოცულობით არადრეკად დეფორმაციაზე, როგორც ეს ნაჩვენებია ნახ. 32-ზე.
ამგვარად მოდიფიცირებული დრაკერ-პრეგერის კაპის დრეკადი მოდელის განსაზღვრა შეიცავს დრეკადობის პარამეტრებს და განმამტკიცებელ პარამეტრებს. დრეკადობის პარამეტრები d, β, R, εplvol |0 (საწყისი მოცულობითი დრეკადი დეფორმაცია), α და k საზღვრავს დენადობის ზედაპირის მოხაზულობას ძაბვების სივრცეში იმ დროს, როდესაც განმამტკიცებელი კანონი განსაზღვრულია ჰიდროსტატიკური კუმშვის დენადობის ძაბვით და მოცულობითი არადრეკადი დეფორმაციით კონსოლიდაციის პროცესის მიმდინარეობისას.
ნახ.32. კაპის განმტკიცება
უწყვეტი ერთზედაპირიანი კაპის პლასტიკური მოდელი. დრაკერის მიერ (1957) დამუშავებული კაპის პლასტიურობის მოდელი ტრადიციულად მოიცავს 2 დამოუკიდებელ უწყვეტ დიფერენცირებად დენადობის ფუნქციას და აყალიბებს დენადობის ზედაპირს, რომელიც ადგენს დრეკადი უბნის ზღვარს. ამ ორი ზედაპირის გადაკვეთისას ჩნდება კუთხეები. დენადობის შემთხვევაში პლასტიკური დეფორმაციის ნაზრდის მდებარეობა ისაზღვრება დენადობის ზედაპირსა და დენადობის ზედაპირზე მდებარე მისი მიმდებარე წერტილების ნორმალების მიხედვით. Gგანმტკიცების ქცევის შემთხვევაში პლასტიკური დეფორმაციის ნაზრდი მოიცავს პლასტიკური დეფორმაციების ნაზრდის ჯამს, გამოთვლილს დამოუკიდებლად თითოეული დენადობის ფუნქციიდან. სანდლერისა და რუბინის (1979) ტრადიციული კაპის პლასტიკური მოდელი ფორმულირებულია 2 ინვარიანტით _ პირველი, I1, არის ძაბვა და მეორე, I2,არის დევიატორული ძაბვა. მთავარი ძაბვებით გამოსახული ეს ინვარიანტები შემდეგნაირად არის გამოსახული /47/:
სადაც σ1≥ σ2 ≥ σ3 და კუმშვა აღებულია უარყოფითად. თუ სიმტკიცე გაჭიმვისას ნაკლებია ვიდრე კუმშვისას, რასაც ზოგჯერ ვხვდებით კლდისათვის ან სხვა მყიფე მასალისათვის, როგორიცაა ბეტონი, მაშინ საჭიროა ზოგადად სამინვარიანტული მოდელი.
ერთზედაპირიანი მოდელი შეიძლება გამოყენებული იქნეს დრეკადი ქცევისათვის, ძვრის ნგრევისათვის და კაპის პლასტიკურობისათვის. ასეთ მოდელში დენადობის ზედაპირი მოიცავს ძვრის დენადობის ფუნქციას და კაპს, რომელიც მტკიცდება (ნახ.33)
ნახ 33. ტრადიციული კაპის პლასტიკურობის მოდელის ძვრის ზედაპირი და გამამტკიცებელი კაპის ზედაპირები.
კაპის ფორმა აღწერილია ელიფსური ზედაპირით შემდეგნაირად:
რომელშიც
X = L - R [A - Cexp(BL)]
კაპის პოზიციის პარამეტრები L და X განსაზღვრავენ მოცემული კაპის ზედაპირის ადგილმდებარეობას. მასალის პარამეტრი, R, განსაზღვრავს კაპის ზედაპირის ელიფსის ძირითადი რადიუსების შეფარდებას. განმამტკიცებელი პარამეტრი, k, ისაზღვრება X(k) ფუნქციონალის და მოცულობითი პლასტიკური დეფორმაციის εv რომელიც ვითარდება მხოლოდ კაპის ზემოქმედებით, საშუალებით.
განხილულ მოდელს გააჩნია მთელი რიგი ნაკლისა, რადგანაც არსებობს გაურკვევლობა პლასტიკური დეფორმაციის მიმართულების გადაკვეთისა ძვრის დანგრევის და კაპის განმამტკიცებელ ზედაპირებთან. ფიზიკური აზრით მოთხოვნა, რომ კაპის განმამტკიცებელმა ზედაპირმა გადაკვეთოს ძვრის დანგრევის ზედაპირი კაპის ელიფსთან ჰორიზონტალური შეხების წერტილში ნიშნავს იმას, რომ პრევენცია გაუკეთდეს დანგრევის წინარე და დილატანსიის დეფორმაციას, რაც ეწინააღმდეგება ექსპერიმენტულ მონაცემებს.
ერთზედაპირიანი უწყვეტი დენადობის ფუნქცია ასეა მოცემული:
სადაც კ არის კაპის განმამტკიცებელი პარამეტრი, αij არის უკუ-ძაბვის ტენზორი, Г არის ლოდეს კუთხის ფუნქცია.
ამ ფუნქციით განსაზღვრული დენადობის ზედაპირის მოხაზულობა მოცემულია ნახ.34-ზე. როცა დენადობის ზედაპირი მტკიცდება, მას გარეთ გამოაქვს ძვრის დანგრევის ზედაპირი, რომელიც მოცემულია ნახ.33-ზე.
ნახ.34. უწყვეტი ერთ-ზედაპირიანი დენადობის ზედაპირები
I1-ის მოცემული მნიშვნელობისას თითოეული გამამტკიცებელი ზედაპირის პიკი, რომელიც წარმოადგენს კრიტიკულ მდგომარეობას, ბევრად დაბლაა, ვიდრე ძვრის დანგრევის მდებარეობის შესაბამისი წერტილი. სწორედ ეს არის ის საშუალება, რომელიც უშვებს დეფორმაციის გადასვლის მოდელირებას გამკვრივებიდან დილატანსიამდე, რომელიც ვითარდება მანამდე, ვიდრე მასალა დაინგრევა ძვრისაგან.
უახლესი თანამედროვე ერთგვაროვანი კაპ მოდელი. სამზედაპირიანი დრაკერ-პრეგერის დანგრევის მრუდი, გნმამტკიცებელი წრიული კუმშვის კაპი და ფიქსირებული გაჭიმვის კაპი იკვეთება მდოვრედ ისე, რომ არ არსებობს კუთხეების უბნები. ამგვარად ასეთი არაერთგვაროვნება თავიდან იცილებს სიძნელეებს, რომლებიც დაკავშირებულია კუთხეების უბნებთან, რომლებიც შეიცავენ: მასალის დამარბილებელ რეაქციას, მასალის მხები ოპერატორების არასრულფასოვნებისა და სინგულარობის ნაკლს. მოდელი გვიჩვენებს არსებითად იგივე რეალიზმის ფიზიკურ ხარისხს, როგორც წინამორბედი კაპ მოდელები, მაგრამ მისი რიცხობრივი წარმოდგენის მახასიათებლები მნიშვნელოვნად გაძლიერებულია.
წარმოდგენილი უახლესი მდოვრე კაპ მოდელისათვის დეტალურად მოცემულია ინტეგრირების ალგორითმი და გამოსახულებები მდგრადი მხები ოპერატორებისათვის. ინტეგრირების ალგორითმი ეფუძნება ეილერის უკუსვლის ძირითადი განტოლებების დიაპაზონს.
იმისათვის, რომ განხილული იყოს ის სირთულეები, რომლებიც დაკავშირებულია მდოვრე დენადობის ზედაპირთან, იგი (ნახ.35) წარმდგენილია 3 ერთგვაროვან ერთმანეთის გადამკვეთ fm(σ, k)(m = 1, 2, 3) დენადობის ზედაპირად /41/. 3 დენადობის ზედაპირის ფუნქციის ფორმა გამოხატულია Fe, Fc and Ft ფუნქციების ფორმით, რომლებსაც ჰქვია დრაკერ-პრეგერის მრუდის ფუნქცია, კუმშვის კაპის ფუნქცია და გაჭიმვის კაპის ფუნქცია.
გრუნტების ბლანტპლასტიკური დეფორმირების კაპ მოდელი. არაბმული და ბმული (D<0,17) გრუნტების პლასტიკური დეფორმირება სტატიკური ზემოქმედებისას შეიძლება განხილული იყოს მოდებული დატვირთვის მიმართ დეფორმაციის დაგვიანების გათვალისწინების გარეშე. ამ შემთხვევაში მხედველობაში არ არის მიღებული გრუნტების რეოლოგიური თვისებები.
ნახ.35. ერთგვაროვანი სამზედაპირიანი ორინვარიანტიანი დენადობის ზედაპირი კაპ მოდელისათვის
პლასტიკური დენადობის თეორიის გამამტკიცებელ გარემოზე დაყრდნობით გრუნტის მათემატიკური (კაპ) მოდელის განმსაზღვრელი თანაფარდობა შემდეგნაირად არის ჩამოყალიბებული: /42/
1. დეფორმაციის სრული ნაზრდი განისაზღვრება შემდეგი ჯამის სახით:
- d ij = d eij + d pij
- d ij = d eij + d pij
სადაც d eij არის ჰუკის კანონის შესაბამისად გამთვლილი დრეკადი დეფორმაციების კომპონენტების ნაზრდი.
- d ij = cpij,ke d σ ke
- d ij = cpij,ke d σ ke
აქ cpij,ke არის განტვირთვის მიხედვით განსაზღვრული დრეკადი მახასიათებლების მატრიცა.
2. პლასტიკური დეფორმაციების d pij ნაზრდი განისაზღვრება დატვირთვის ზედაპირის fr=0 ყველა რეგულარული უბნის დეფორმაციების ნაზრდის ჯამით:
- d pij = Σ dλr
- d pij = Σ dλr
სადაც dλr – პლასტიკური მამრავლებია.
ამ შემთხვევაში მიღებულია კოიტერის პლასტიკური დენადობის ასოცირებული კანონი, როცა დრეკადი დეფორმირების არე ემთხვევა დატვირთვის ზედაპირს fr=0, რომელსაც გააჩნია რეგულარული უბნები და განსაკუთრებული (სინგულარული) წერტილები A-F. ნახ.36-ზე ძაბვების სივრცეში, დატვირთვის ზედაპირით შემოსაზღვრული, მოცემული არის ფიზიკური არსი მდგომარეობს იმაში, რომ ამ არის საზღვრებში გრუნტი იქცევა როგორც დრეკადი. იმ შემთხვევაში, თუ დატვირთვა გამოდის ამ არის გარეთ, ვითარდება ძვრის და მოცულობის შეუქცევადი პლასტიკური დეფორმაციები, რომლებიც ხასიათდებიან ეპი და პვ ინვარიანტებით. Kკოიტერის წესი, რომლის მიხედვითაც ისაზღვრება პლასტიკური დეფორმაციების ნაზრდი, ისაზღვრება ზემოთ მოყვანილი ფორმულით. დატვირთვის ზედაპირის მდებარეობა იცვლება დეფორმირების პროცესში პლასტიკური დეფორმაციების დაგროვების მიხედვით. დატვირთვის ფუნქციას შემდეგი სახე აქვს: fr = fr(σi; σ; ωi; ωv; kr), სადაც kr არის რეგულარული უბნების მახასიათებელი მუდმივები; ωi; ωv არის განმტკიცების პარამეტრები. დატვირთვის ზედაპირის კვალი შედგება 4 რეგულარული უბნისაგან და გააჩნია რიგი სინგულარული წერტილისა, რომლებზეც ხდება მხების წყვეტა. პირველი უბნის გარდა, როცა fr=1=0 (უბანი BAB) და შეესაბამება გრუნტის წინაღობას მოწყვეტის მიმართ, ყველა დანარჩენი უბანი (BC, CD, DF) პლასტიკური დეფორმაციების განვითარების პროცესში იცვლიან თავის მდებარეობას - პლასტიკურად განმტკიცებული არე. დატვირთვის ზედაპირის შეცვლის კანონზომიერება ისაზღვრება განმტკიცების ფუნქციებით, რომლებიც დამოკიდებულია დაგროვილი პლასტიკური დეფორმაციებისაგან-განმტკიცების პარამეტრებისაგან.
ამგვარად გრუნტის დატვირთვისას წარმოიქმნება საწყისი ზედაპირი, რომელიც ჰიდროსტატიკური დაწნევის ტრაექტორიის მიხედვით დატვირთვისას შემოზღუდავს არეს, რომლის შიგნით ძვრის ძაბვები არ გამოიწვევნ ძვრის პლასტიკური დეფორმაციის დაგროვებას, ანუ იგი ახასიათებს გრუნტის სტრუქტურულ სიმტკიცეს რთული დაძაბული მდგომარეობის პირობებში, რომელიც ჩნდება წინასწარი ყოველმხრივი მოკუმშვის შედეგად. /42/
LS-DYNA სახელმძღვანელოში გამოყენებული კაპ მოდელი. ნახ.37-ზე მოცემულია გამოყენებული ორი მოდელი დენადობის ზედაპირისათვის მთავარ ძაბვების ღერძებში. წამყვანი ღერძი ყოველი ზედაპირისათვის არის დაწნევის ღერძი. მარცხნივ - ა) არის მორ-კულონის მოდელი (ტიპური გრუნტის დენადობის ზედაპირი) და შედარებისთვის მარჯვნივ - ბ) არის სტანდარტული ფონ მიზესის მოდელი (ტიპური ლითონის დენადობის ზედაპირი). /44,49/ გრუნტის დენადობა (პლასტიკურობის დაწყება) და ზღვრული (პიკური) სიმტკიცე დამოკიდებულია დაწნევაზე, რაც იმას ნიშნავს, რომ პლასტიკურობის ზედაპირი დამოკიდებულია როგორც დაწნევაზე, ასევე ძვრის ძაბვებზე. ლითონში კი - პლასტიკურობის ზედაპირი მხოლოდ ძვრის ძაბვების ფუნქციაა. ექსპერიმენტული მონაცემებით შეჭიდულობის არამქონე გრუნტისათვის დაბალი
ნახ.36.დატვირთვის ზედაპირის განვითარება პლასტიკური დეფორმირების პროცესში ა) და ძვრის დიაგრამა ბ).1-დატვირთვის საწყისი ზედაპირი. 11–111 – დატვირთვის ზედაპირის მდგომარეობა პლასტიკური დეფორმაციების ფიქსირებული მნიშვნელობების დროს.
დაწნევის მნიშვნელობისას დენადობის ზედაპირი დევიატორულ სიბრტყეში სამკუთხაა (ნახ.38) და მინიმალური ძაბვის (სამღერძა გაფართოებისას) შეფარდება მაქსიმალურ ძაბვასთან (სამღერძა კუმშვა) დევიატორულ სიბრტყეში ტოლია 0,70.

|

|
ნახ.37. დაწნევაზე დამოკიდებული სტანდარტული მორ-კულონის დენადობის ზედაპირი მთავარი ძაბვების სივრცეში (სამღერძა გაჭიმვის სიმტკიცის შეფარდება სამღერძა კუმშვის სიმტკიცესთან e=1, წრიული კონუსის შემთხვევა) (ა) და დაწნევაზე დამოუკიდებელი (ფონ მიზესის) ლითონის დენადობის ზედაპირი (ბ).
ნახ.38. დენადობის ზედაპირი დევიატორულ სიბრტყეში შეჭიდულობის არამქონე გრუნტისთვის
დაბალი შეზღუდული დაწნევისას სტანდარტული გრუნტი განიცდის დილატანსიას (ფართოვდება) პიკური ძვრის ძაბვების ახლოს. მაღალი შეზღუდული დაწნევისას (>100 MPa) კი იგი წყვეტს გაფართოებას. სწორედ ცვლილება მოცულობით ქცევაში არის ერთერთი მიზეზი კაპ მოდელის გამოყენებისა. სრული ასოცირებული პლასტიკური მოდელი იძლევა საშუალებას წინასწარ განსაზღვროს მასალის დილატანსიის სურათი მას შემდეგ, რაც დენადობის სიმტკიცე მიღწეულია. სტანდარტული გრუნტი დაბალი შეზღუდული დაწნევით <30MPa აჩვენებს ტიპიურ დეფორმაციის დარბილებას. გრუნტის დეფორმაცია მტკიცდება დენადობის ძაბვიდან ზღვრულ ძაბვამდე, რის შემდეგ დეფორმაცია რბილდება. სწორედ ეს დარბილება შეიძლება იყოს უმთავრესი წყარო ენერგიის დისიპაციისა. ამიტომ ის უნდა იყო შეყვანილი მასალის მოდელში.
სტანდარტული მორ-კულონის დენადობის ზედაპირი, რომელიც წარმოადგენს ან ექვსკუთხედს ან წრეს დევიატორულ სიბრტყეში, მოცემულია ასე:
სადაც P დაწნევაა; φ – შიდა ხახუნის კუთხეა; K(θ) არის ხახუნის კუთხე θ დევიატორულ სიბრტყეში; √I2 არის კვადრატული ფესვი ძაბვების დევიატორის მეორე ინვარიანტიდან; c – შეჭიდულობაა. მაგრამ ცდების მიხედვით ზედაპირი უნდა იყოს სამკუთხა ფორმის დაბალი შეზღუდული დაწნევის შემთხვევაში. ამიტომ მოდიფიცირებული მორ-კულონის დენადობის ზედაპირისთვის გამოყენებულია ჰიპერბოლა, როცა ის კვეთავს დაწნევის ღერძს (ძვრის სიმტკიცე ნულის ტოლია) და მოდიფიცირებული ზედაპირი მდოვრეა. გადაკვეთის წერტილში ის პერპენდიკულარულია დაწნევის ღერძისადმი და ასეთი ზედაპირი ჩაიწერება ასე:
პარამეტრი, რომელიც აქ შეყვანილია, საზღვრავს, თუ რამდენად შეესაბამება მოდიფიცირებული მორ-კულონის ზედაპირი სტანდარტულ მორ-კულონის ზედაპირს. თუ ის ნულია, Mმაშინ აღდგება სტანდარტული მორ-კულონის ზედაპირი. ეს პარამეტრი ახლოს უნდა იყოს ნულთან. მოდიფიცირებული მორ-კულონის ზედაპირი (ძვრის ძაბვა-დაწნევის სიბრტყე) იდენტურია ორიგინალური ზედაპირისა მხოლოდ დაბალი ძაბვების შემთხვევაში.
დევიატორულ სიბრტყეში დენადობის ზედაპირის ფორმის მისაღებად სტანდარტულ მორ-კულონის K(θ) ფუნქცია შეცვლილია შემდეგი ფუნქციით:
- სადაც
არის ძაბვების დევიატორის მესამე ინვარიანტი და ე არის მასალის შესაყვანი პარამეტრი, რომელიც ტოლია სამღერძა გაჭიმვის სიმტკიცის შეფარდებისა სამღერძა კუმშვის სიმტკიცესთან. თუ e=1, მაშინ ჩამოყალიბდება წრიული კონუსის ზედაპირი (ნახ.37) და თუ e=0,55, მაშინ ზედაპირი იქნება სამკუთხა (ნახ.39). K(θ) ისაზღვრება 0,5<e≤1,0 -სთვის
ნახ.39. დენადობის ზედაპირი, როცა e=0,55
დენადობის ზედაპირის განმტკიცების სიდიდე იზრდება გვერდული შეზღუდვის გაზრდით (მაგ. თუ არსებობს დაბალი შეზღუდული დაწნევა, მაშინ განმტკიცება ნაკლებია). არაწრფივი განმტკიცების ქცევის მოდელირებისათვის უნდა მოხდეს ხახუნის კუთხის გაზრდა პლასტიკური ეფექტური დეფორმაციის ფუნქციაზე დამოკიდებულებით. (ნახ.40)
ნახ.40. დენადობის ზედაპირის განმტკიცება
დრაკერ-პრეგერისა და მორ-კულონის კომბინირებული მეთოდი.ამ შემთხვევაში ხდება მორ-კულონის კრიტერიუმის დრაკერ-პრეგერის მოდელით მდოვრე აპროქსიმაცია, რაც საშუალებას იძლევა ის გამოყენებული იყოს ძვრის კაპ მოდელში. /50/.Uუდიდესი უპირატესობა ძვრის კაპ-მოდელისა ამ ორ მოდელთან შედარებით არის ის, რომ ის აძლევს მასალას საშუალებას დაინგრეს გამკვრივებისას ისევე კარგად, როგორც ძვრისას. მდოვრე დენადობის ზედაპირი იქმნება ორი ელიფსური დენადობის ზედაპირისგან, როგორც ეს ნაჩვენებია ნახ.41-ზე. ერთი ზედაპირი არის ძვრის დანგრევისთვის და მეორე - დანგრევის კაპისათვის, რომელიც იძლევა გამკვრივების დანგრევას.
დენადობის ფუნქცია კაპის ნგრევისათვის იქნება:
ნახ.41.ძვრის კაპის დენადობის ფუნქცია მერიდიანულ სიბრტყეში
სადაც pb (ჰიდროსტატიკური დაწნევის სიმტკიცე) წარმოადგენს კაპის განმტკიცების კანონს შემდეგნაირად:
და pa განსაზღვრავს დაწნევას, რომელიც ჰყოფს ძვრის კაპის დენადობის ზედაპირს ორ ნაწილად:
სადაც d არის შეჭიდულობის პარამეტრი დრაკერ-პრეგერის მოდელში; R განსაზღვრავს კაპის მოხაზულობას; ko არის კაპის გამამტკიცებელი პარამეტრი; ε არის ბაზური მოცულობითი პლასტიკური დეფორმაცია კაპის განმამტკიცებელ მოდელში; β არის შიდა ხახუნის კუთხე დრაკერ-პრეგერის მოდელში; q არის დევატორული ძაბვის მეორე ინვარიანტი. როცა დაწნევა მეტია, ვიდრე pa, ხდება გამკვრივება, რაც ზრდის შიდა წილობრივ საკონტაქტო ძალებს. ეს ის შემთხვევაა კაპის დანგრევისა, როცა მასალა მტკიცდება. განმტკიცების პარამეტრი დენადობის ზედაპირში არის პა, რომლის დამოკიდებულება pb-ზე მოცემულია ზემოთ. კაპის განმამტკიცებელ კანონზე დაყრდნობით, განმტკიცება ან დარბილება მასალისა დამოკიდებულია მოცულობით პლასტიკურ დეფორმაციაზე. დენადობის ზედაპირის ზომა კონტროლდება მასალის მარეგულირებელი პარამეტრის pa–ს მიხედვით. როცა ძაბვები განლაგებულია კაპის მხარეს, მოცულობითი პლასტიკური დეფორმაცია უარყოფითია და მასალა მკვრივდება და დენადობის ზედაპირი იზრდება. როცა ძაბვები განლაგებულია ძვრის დანგრევის მხარეს, მაშინ მოცულობა იზრდება, რაც იწვევს დენადობის ზედაპირის კუმშვას.
დანართი 1. ქ. თბილისში „სატივეს“ მშენებარე ფერდობის სტატიკური და სეისმური მდგრადობის ანგარიში
განსახილველი ფერდობი წარმოადგენს სტრუქტურას, რომელშიც ენაცვლება ფერდობის შემადგენელი 2 ძირითადი ფენა - 20სმ სისქის ქვიშაქვა 2სმ არგელიტის შუა შრეებით. ფენები პარალელურია და ჰორიზონტთან დახრილია 290-ით. ფერდობის შესაძლო მდგრადობის დაკარგვის სქემა შეიძლება წარმოდგენილი იყოს როგორც ქვიშაქვის ფენების სრიალი არგელიტის შუაშრეებზე. ფერდობის მდგრადობის გაანგარიშებისათვის შერჩეული იქნა სასრულო ელემენტის მეთოდი. განიხილებოდა ფერდობის ბრტყელი-დეფორმირებული მოდელი გეომეტრიული არაწრფივობის გათვალისწინებით /37/. განსაკუთრებული ყურადღება მიექცა იმ კონტაქტების მოდელირებას, რომელიც არსებობს ქვაქვიშების ფენებს შორის და რომელშიც ჩართულია არგელიტის შუაშრეები. საანგარიშო სქემაში ქვაქვიშების ფენების სისქე გაზრდილია 1÷1,5-მდე. შუაშრეები გათვალისწინებულია მოდელში მხოლოდ მასივის აქტიურ ზონაში 16 შესაძლო დაცურების ხაზით, რომლებიც კვეთავენ ფერდობის მასივს 40მ-ის სიღრმეზე. დაცურების თითოეული ხაზი მოდელირებულია 90-110 სპეციალური სასრულო ელემენტის საკონტაქტო წყვილით, რომელთა საკონტაქტო სიმტკიცე განპირობებულია არგელიტების ფიზიკო-მექანიკური მახასიათებლებით. მასივის ტანი აღწერილია სამ და ოთკუთხა 8 კვანძიანი არაწრფივი სასრულო ელემენტით, რომელიც ხასიათდება გრუნტის მასივის ფიზიკო-მექანიკური პარამეტრებით (ნახ.1-1). რადგანაც გეოლოგიური მონაცემები შეზღუდული იყო თავის გაბარიტულ ზომებში და ისინი საკმარისი არ იყო სარწმუნო თეორიული კვლევებისათვის, ამიტომ გაბარიტები გაზრდილი იყო სიგრძეში - 200მ-მდე და სიმაღლეში – 90მ-მდე.ამავე დროს შენარჩუნებული იყო გრუნტის მასივის სტრუქტურული თავისებურებანი. ყველა გეომეტრიული და სიხისტის მახასიათებლები და აგრეთვე შესაბამისი გარე დატვირთვა ითვლებოდა ფერდობის 1 მეტრიანი ზოლისათვის. მდგრადობის ამოცანა გადაწყვეტილი იყო ფერდობზე მშენებარე ნაგებობისა და თვით ფერდობის ურთიერთზემოქმედების გათვალისწინებით. შენობის კარკასის ექვივალენტური მოდელი აღწერილი იყო ღეროვანი სასრულო ელემენტით. სეისმური თანაბარგანაწილებული დატვირთვა იგულისხმებოდა მოდებულად ჩარჩოს რიგელის დონეზე.
ნახ.1-1. ფერდობის მდგრადობის საანგარიშო სასრულო ელემენტიანი სქემა
8 ბალიანი მიწისძვრისგან გამოწვეული შენობის ინერცია, რომელიც გადაეცემოდა გრუნტის მასივს, განსაზღვრული იყო მოქმედი სეისმური ნორმეBით /38/. განიხილებოდა საძირკველში ხისტად ჩამაგრებული ცალკე მდგომი კარკასი. ასეთი სქემის შერჩევა განაპირობა იმან, რომ არ არსებობდა განსახილველი ადგილმდებარეობისათვის რეკომენდებული რეალური აქსელეროგრამის ჩანაწერები არაწრფივი გაანგარიშებისათვის. ფერდობის გამოთვლილი უსაფრთხოების ფაქტორის სიდიდე იცვლებოდა F=1,5÷2,5-ის ფარგლებში.
რადგანაც ობიექტი რეალური იყო, ამიტომ დაშვებებების სამართლიანობის შესამოწმებლად მიზანშეწონილად ჩაითვალა იგივე ამოცანა გადაწყვეტილიყო სღვრული წონასწორობის მეთოდით /35/. დატვირთვები და ზემოქმედებები მოდელირებული იყო შემდეგნაირად: ვერტიკალურ დატვირთვაში შეტანილი იყო ფუძის გრუნტის მასები მათი სიმტკიცის მიხედვით. დატვირთვა შენობისაგან, რომელიც გადაეცემოდა ფუძეს საძირკვლის მეშვეობით, მოდელირებული იყო გრუნტის ექვივალენტური მოცულობითი სიმკვრივით 50კნ/მ3. გრავიტაციული დატვირთვების გარდა გათვალისწინებული იყო დინამიური ინერციული ზემოქმედება 8 ბალიანი სეისმური ზემოქმედების ვერტიკალური მდგენელის სახით, აჩქარების ინტენსიურობით a=0,05g /9/-ის მიხედვით. ჰორიზონტალურ დატვირთვაში იგულისხმებოდა მხოლოდ 8 ბალიანი სეისმური ზემოქმედების ინერციული მდგენელი, აჩქარებით a=0,1g.
ფერდობის მდგრადობის შემოწმება ზღვრული წონასწორობის მეთიდით ტარდებოდა შემდეგნაირად: წინასწარ ინიშნებოდა ზედაპირის დაცურების ხაზები როგორც წრიული, ასევე ტეხილი ფორმის და მათ მიხედვით ისაზღვრებოდა შესაბამისი უსაფრთხოების ფაქტორის სიდიდეები.
შემოწმებული იყო ყველა ფორმისა და სიგრძის ზედაპირის 602 დაცურების ხაზის უსაფრთხოების ფაქტორის სიდიდე. მიღებული მნიშვნელობა ერთერთი ხაზისათვის არის F=1,43. ნახ.1-2-ზე მოცემულია ზღვრული წონასწორობის მეთოდის შესაბამისი ერთერთი საანგარიშო სქემა.
ნახ.1-2. ფერდობის მდგრადობის საანგარიშო სქემა ზღვრული წონასწორობის მეთოდით
გამოყენებული ლიტერატურა
- ОкамотоШ.Сейсмостойкостьинженерныхсооружений.Стройиздат.Москва.1980.342c.
- Kyriakos Kyrou.Seismic Slope Stability Analysis. pdf?Open Element
- Slope Stability Engineer Manual. US Army Corps of Engineers. Engineering and Design. [http.//www.usace.army.mil/inet/usace-docs/.31 oct.2003]
- Sarma K.Sarada. Stability Analysis of Embankments and Slopes. J. Geotechnical Engineering Division. GT12, December,1979.p.p.1511-1524.
- Melo Cristiano and Sharma Sunil. Seismic Coefficient for Pseudo-static Slop Stability Analysis. 13th WCEE. Vancouver, Canada, August,1-4, 2004. paper N369.
- Pyke Robert. Selection of Seismic Coefficients for use in Pseudo-ststic Slope Stability Analysis. [http.//www.tagasoft.com./TAGAsoft/Discussion/article 2-html]
- Seismic Coefficient for Slope Stability. Eng.TipsForum. [http.//www.engtips.com./view.thread.cfm?qid=33157]
- Makdisi F.L. and Seed H.B. Simplified Procedure for Estimating Dam and Embankment Earthquake Induced Deformations. J. Geotechnikal Engineering Division. vol.104.NG17.1978. p. 849-867.
- Рекомендации по количественной оценке устойчивости оползневых склонов»,ПНИИС Госстроя СССР,Москва,1984
- Timothy Stark, Philip O’Leary and Patrik Walsh. Static and Seismic Stability of Landfill Slopes. Waste Age. [1]
- Rao Suhba K.S. Design of Earthquake Dams under Dynamic Loading Conditions.
- Seed Bolton H., Makdisi Faiz J. and De Alba Pedro. Performance of Earth Dams During Earthquakes. J. Geotechnical Engineering Division. vol.104.NGT7, July,1978. p.p. 967-994.
- Miyajima M. Damage Analysis of Buried Lifelines in the Niigata-Ken Chuetsu Earthquake, Japan. 8th NCEE, April 18-22,2006, San Francisko, California, USA. paper N1042.
- Seed Bolton H. Landslides During Earthquake due to Soil Liquafaction. J. Soil Mechanics and Foundations Division. vol.94. NO.SM5.Sept.1968. p.p. 1055-1123.
- Castro Gonzalo, Poulus Steve J. and Leathers Francis D. Re-Examination of Slide of Lower San Fernando Dam. J. Geotechnical Engineering. vol.111.NO9. Sep.1985. p.p. 1093-1107.
- ცისკრელი ციალა. მიწისქვეშა მაგისტრალური მილსადენების სეისმომედეგობა. თბილისი, 2003.130გვ.
- Bilge Gokmirza Siyahi and Atilla M.Ansal. Slope Instability During Earthquakes. 10th ECEE,Duma,1995, Belkema, Rotterdam. p.p.515-519.
- Seed H.B. and Idriss I.M. Simplified Procedure for Evaluating Soil Liquafaction Potential. J. Soil Mechanics and Foundations Division. vol.97.NSM9,1971. p.p.1243-1273.
- Seed H.B. Soil Liquafaction and Cyclic Mobility Evalution for Level Ground During Earthquakes. J. Geotechnical Engineering Division. vol.105.NGT2.1979. p.p.201-255.
- Rollins Kyle M and Seed Bolton H. Influence of Buildings om Potential Liquafaction Dammage. J. Geotechnical Engineering. vol 116. NO2. Feb.1990. p.p.165-185.
- Shukha Robert, Baker Rafael, Leshchinsky Dov. Engineering Implication of the Relation Between Static and Pseudo-Static Slope Sttability Analysis. http://www.ejge.com./2005/Ppr0616/Ppr 0616.htm.
- Newmark N. Effects of Earthquakes on Dams and Embankments. Geotechnique, vol.15.NO2,p.p. 139-160.
- Spenser E. Effect of Tension on Stability of Embankments. J. Soil Mechanics and Foundation Division. vol.94.NO.SM5.Sept.1968.pp.1159-1173.
- Seed H.B., Idriss I.M., Ignasio Arango. Evolution of Liquafaction Potential using Field Performance Data. J.”Geotechnical Engineering”, vol.109,N3,1985.pp.458-482.
- Kramer I.Steven, See3d H.B. Initiation oof Soil Liquafaction under Loading Conditions. J.”Geotechnical Engineering”,vol.114, N4.1988.pp 412-430.
- Blazquez R. Liquafaction Modelling in Engineering Practice. 10th European Conference on Earthquake Engineering.Vienna,Austria.1994.pp.501-513.
- Seed H.B.,K.Tokimatsu, L.F.Harder, Riley M.Chung. Influence of SPT Procedures in Soil Liquafaction Resistance Evaluation. J.”geotechnikal Engineering”,vol.111,N12,1985.pp.1425-1445.
- Eurocode 8: Design of Structures for Earthquake Resistance. Part 5: Foundations, retaining structures and geotechnical aspects. EN 1998-5:2004. October 2003. 44p.
- Eurocode 8: Design of Structures for Earthquake Resistance. Part 1. General rules, seismic actions and rules for buildings. EN 1998 – 1:2004. November 2004. 229p.
- General Slope Stability Concepts. www.loc.gov./catdir/samples/wiley 031/2001026917. 25p.
- Reinforced Soil Slopes and Embankments. www.geogrid.com./pdf/slopesman.pdf. 44p.
- Geotechnical Design Manual M 46-03, Seismic Design. Chapter 6.December,2006. Publications/Manuals/GDM/Chapter 6.pdf1530k. 48p.
- Recommended Procedures for Implementation. Draft.2005. 117 slope.pdf
- Guidelines for Evaluiting and Mitigating Seismic Hazards in California,1997. Special Publication 117. docs/
- Sarma S.K. Stability Analysis of Embankments and Slopes. Geotechnique,23.N3.1973.p.p. 423-433.
- Geotechnical Analysis and Design. Chapter 6. CHP 6%20 final.pdf.
- Чхиквадзе К., Цискрели Ц.,Члаидзе Н. Численное исследование сейсмической устойчивости застраиваемого склона «Сативе» в г. Тбилиси. VI Всеукраинская н-тех. конференция «Стр-во в сейсмических р-нах Украины». Ялта,25-29 сентября,2006.
- Строительные Нормы и Правила,СНиП П-7-81.Строительство в сейсмичсеких районах. Москва,1982. 50с.
- კიზირია გ., ჯანელიძე შ., გრიგოლია ნ. შენობა-ნაგებობათა ავარიები, აღდგენა-გაძლიერება და ახალი კონსტრუქციები. თბილის,1996. 250გვ.
- Bojorque J., De Roeck G. Determination of the critical seismic acceleration coeffocoent in slope stability analysis using finite element methods. jaime, bojorque@bwk.kuleuven.be.
- Colby C. Swan, Young-Kyo Seo. A Smooth, Three-Surface Elasto-Plastic Cap Model: Rate Formulation, Interpretation, Algorithm and Tangent Operators. www.icaen.uiowa.edu/-swan/geomech/geomech_papers/capmod-246k-view.
- Зарецкий Ю.К.Вязко-пластичность грунтов и расчеты сооружений. Стройиздат, М. 1988.350 с.
- Akers A. Stephen. Two-Dimensional Finite Element Analysis of Porous Geomaterials of Multikilobar Stress Levels. Dissertation submitted to the Faculty of the Virginia Politechnic Institute and State University, December,7,2001. Chapter 4. Cap Models and its Implementation. [2]
- Mat.Geologic Cap Model –LS-DYNA,Version 950.mk@MSITStore: C\Program%20Files\Ansys%20Inc\ANSYS60\do…/HEP_L_mat13.htm. 09.09.2002.
- Филин А.П.Прикладная механика твердого деформируемого тела.т1.Наука.1975.398с.
- Gautam S.Wagle, Renata S.Engel, Ravi Bollina and Randall M.German. Statistical Analysis of Modified Drucker-Prager Parameters for Application to Modeling Die Compaction. [3]
- Fossum A.F. and Fredrich J.T. Cap Plasticity Models and Compactive and Dilatant Pre-feilureDeformation. [4]
- Работнов Ю.Н. Механика деформируемого твердого тела. М.Наука. 1979. 744 с.
- Manual for LSDYNA Soil MaterialModel147. [5].
- Mohamed O.ElSeify and Thomas G.Brown. Introducing the Shear-Cap Material Criterion to an Ice Rubble Load Model. PERD/IAHR_06_shear_cap_model.pdf