ფერდობების სტატიკური მდგრადობის განსაზღვრისათვის გამოყენებული საანგარიშო მეთოდები
ზღვრული წონასწორობის მეთოდი
[რედაქტირება]ფერდობის სტატიკური მდგრადობის ხარისხის განმსაზღვრელად მიღებულია მდგრადობის მარაგის კოეფიციენტი, ანუ უსაფრთხოების ფაქტორი, F, რომელიც წარმოადგენს სიდიდეს პოტენციალური ძვრისადმი წინაღობის ძალების ფარდობისა იმ აქტიურ ძალებთან, რომლებსაც შეუძლიათ გამოიწვიონ გრუნტის დაცურება. მისი გამოთვლა შესაძლებელია ძვრის სიმტკიცის, S, შეფარდებით წონასწორობისთვის საჭირო ძვრის ძაბვასთან, τ.
- F = S / τ = c’ + (σ -u) tan φ’ (6)
- აქ c’ არის შეჭიდულობა;
- φ’ არის ხახუნის კუთხე;
- σ არის ჩამონგრევის სიბრტყის მთლიანი ნორმალური ძაბვა;
- u არის წყლის ფოროვანი დაწნევა;
(σ -u) არის ეფექტური ნირმალური ძაბვა დანგრევის სიბრტყეში.
უსაფრთხოების ფაქტორის გამოთვლა ხორციელდება ზღვრული წონასწორობის სხვადასხვა მეთოდის საშუალებით სტატიკური წონასწორობის ერთი ან მეტი განტოლების გამოყენებით, იმ გრუნტის მასების დაყოფით ვერტიკალური ბლოკების სასრულო რიცხვით, რომლებიც განთავსებულია დაცურების ზედაპირის ზემოთ. ამ მეთოდებში არსებობს 2 ტიპის გადაწყვეტა: “გამარტივებული”,რომელშიც სტატიკური წონასწორობის მდგომარეობა მკაცრად არ კმაყოფილდება და დაშვებები კეთდება მარტივი ფორმით ანგარიშის მისაღებად და “ზუსტი”, რომელშიც წონასწორობის მდგომარეობა მთლიანად კმაყოფილდება დასაშვები სიდიდით /4/.
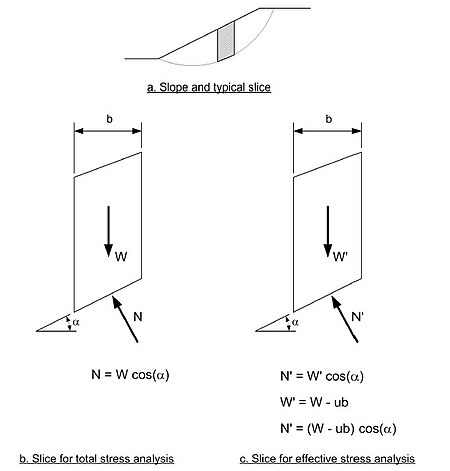
ძალები, რომლებიც ჩვეულებრივად მოქმედებენ ინდივიდუალურად ბლოკზე, მოცემულია ნახ. -ზე.
- აქ W არის ბლოკის წონა;
- E არის ჰორიზონტალური (ნორმალური) ძალები ბლოკის გვერდებზე;
- X არის ვერტიკალური (ძვრის) ძალები ბლოკებს შორის
ნახ.6. ტიპური ბლოკი და ძალები ბლოკთა მეთოდისათვის
- N არის ნორმალური ძალა ბლოკის ძირში;
- S არის ძვრის ძალა ბლოკის ძირში.
გარდა ბლოკის წონისა, ყველა ძალა უცნობია და ისინი ისე უნდა გამოითვალოს, რომ დაკმაყოფილდეს სტატიკური წონასწორობა.
ძვრის ძალა, S, ბლოკის ძირში პირდაპირ არ განიხილება როგორც უცნობი წონასწორობის განტოლებაში და მისი გამოსახვა შესაძლებელია სხვა ცნობილი და უცნობი სიდიდეებით ასე:
- S= τΔl (7)
- სადაც τ არის ძვრის ძაბვა;
- Δl არის ბლოკის ძირის სიგრძე
ნორმალური ძალა, N, ტოლია ნორმალური ძაბვის, σ, ნამრავლისა ბლოკის ძირის, Δl, სიგრძეზე, ანუ
- N = σ Δl (8)
- (6)-დან ისაზღვრება τ
- τ = c’ + (σ -u) tan φ’ / F (9)
- მაშინ
- S = c’ Δl / F + (N-uΔl) tan φ’ /F (10)
ამგვარად ძვრის ძალის განსაზღვრა შეიძლება მოხდეს (9)-დან. დანარჩენი უცნობები და ძალები, რომლებიც უნდა განისაზღვროს წონასწორობის განტოლებიდან, მოცემულია 4 ცხრილში.
ცხრილი 4
უცნობები და განტოლებები ზღვრული წონასწორობის მეთოდისათვის
|
იმისათვის, რომ დამყარდეს ბალანსი უცნობების რიცხვსა და წონასწორობის განტოლებების რიცხვს შორის (როგორც 4 ცხრილიდან ჩანს, განტოლებების რიცხვი 3n ნაკლებია უცნობების რიცხვზე (5n-2)-ზე, საჭიროა გაკეთდეს ზოგიერთი დაშვება, რათა მოხდეს ამოცანის გადაწყვეტა. ეს დაშვებებია:
- უსაფრთხოების ფაქტორის სიდიდე მუდმივია დაცურების ზედაპირის გასწვრივ, თუმცა ფაქტიურად ეს ასე არ არის.
- ყველა ზღვრული წონასწორობის მეთოდი თხოულობს პოტენციალური დაცურების ზედაპირის მოხაზულობის განსაზღვრას უსაფრთხოების ფაქტორის მიხედვით. ამ მოხაზულობის შერჩევა გრძელდება მანამდე, სანამ არ განისაზღვრება დაცვის ფაქტორის მინიმალური სიდიდე. ანგარიშის გამარტივებისათვის დაცურების ზედაპირს განსაზღვრავენ როგორც წრიულს ან შედგენილს მცირე სწორი ხაზებისაგან.
- წრიული დაცურების ზედაპირი ხშირად გამოიყენება, რადგანაც ის მოხერხებულია წრის ცენტრის მიმართ მომენტების შეჯამებისათვის, ამავე დროს ასეთი ზედაპირი ამარტივებს ანგარიშებს.
ბლოკების ჩვეულებრივი მეთოდი
[რედაქტირება]მეთოდი განავითარა ფელენიუსმა (1936) და ზოგჯერ მას „ფელენიუსის“ მეთოდი ეწოდება. ამ მეთოდის მიხედვით ბლოკის გვერდებზე მოქმედი ძალები უგულებელყოფილია (ნახ.7). ნორმალური ძალა ბლოკის ფუძეზე გამოითვლება ძალების ჯამით ბლოკის ძირის პერპენდიკულარული მიმართულებით. როცა ნორმალური ძალა გამოითვლება, მომენტები შეჯამდება წრის ცენტრის გარშემო, რათა განისაზღვროს უსაფრთხოების ფაქტორი. ნახ.-ზე მოცემული ბლოკისათვის და ძალებისათვის უსაფრთხოების ფაქტორი შემდეგნაირად გამოითვლება: /3/
- F =Σ [c’ Δl + (Wcosα – u Δl cos2α ) tan φ’ ] / ΣWsin α (11)
- სადაც c’ და φ’ არის ძვრის სიმტკიცის პარამეტრები ბლოკის ძირის ცენტრის მიმართ;
- W არის ბლოკის წონა;
- α არის ბლოკის ძირის დახრის კუთხე;
- u არის წყლის ფოროვანი დაწნევა ბლოკის ძირის ცენტრის მიმართ;
- Δl არის ბლოკის ძირის სიგრძე.
5 ცხრილში მოცემულია უცნობებისა და განტოლებების რიცხვი, რომელიც საჭიროა ამ მეთოდისათვის.
ცხრილი 5
უცნობები და განტოლებები ფელენიუსის მეთოდისათვის
|
ნახ.7. ტიპური ბლოკი და ძალები ბლოკების ჩვეულებრივი მეთოდისათვის a) ფერდობი და ტიპური ბლოკი; b) ბლოკი მთლიანი ძაბვების საანგარიშოდ; c) ბლოკი ეფექტური ძაბვების საანგარიშოდ.
ამ მეთოდში ბლოკის გვერდებზე მოქმედი ძალები უგულვებელყოფილია. მეთოდი აგრეთვე არ აკმაყოფილებს ძალების წონასწორობის პირობას არც ვერტიკალური და არც ჰორიზონტალური მიმართულებით. მომენტთა წონასწორობა კმაყოფილდება მთლიანი მასისათვის დაცურების ზედაპირის ზემოთ, მაგრამ არა ინდივიდუალურად ბლოკისათვის. ამ მეთოდით გამოთვლილი უსაფრთხოების ფაქტორი შეიძლება თითქმის 20%-ით განსხვავდებოდეს ზუსტი მეთოდით გამოთვლილი მნიშვნელობიდან. ეს მეთოდი გამოიყენება მხოლოდ დაცურების წრიული მოხაზულობისათვის. სიმარტივის გამო ამ მეთოდით ანგარიში კალკულატორითაც შეიძლება.
ბიშოფის გამარტივებული მეთოდი
[რედაქტირება]მეთოდი განავითარა ბიშოფმა (1955) და იგი ეფუძნება იმ დაშვებას, რომ ბლოკებს შორის ძალები, E, ჰორიზონტალურია (ნახ. 8). დაცურების ზედაპირი მიღებულია წრიულად. მოქმედი ძალები ჯამდება ვერტიკალური მიმართულებით. უსაფრთხოების ფაქტორი მიიღება შემდეგი გამოსახულებით: /3/
- F = { Σ [c’Δ x + (W+Pcosβ –u Δxsecα )tan φ’] / mα } / Σ Wsin α – Mp/R (12)
- აქ Δx არის ბლოკის სიგანე და mα განისაზღვრება შემდეგი განტოლებით:
- mα = cosα + sinα tan φ’/F (13)
- აქ P არის წყლის ძალის ტოლქმედი, რომელიც მოქმედებს ბლოკის წვერზე;
- Mp არის შესაბამისად მისი მომენტი. დანარჩენი ცნობილია ნახაზიდან.
უსაფრთხოების ფაქტორი, გამოთვლილი (11)-დან, აკმაყოფილებს ძალების წონასწორობას ვერტიკალური მიმართულებით და მომენტების წონასწორობას წრის ცენტრის გარშემო. უცნობები და განტოლებები ბიშოფის გამარტივებული მეთოდისათვის მოცემულია 6 ცხრილში.
ცხრილი 6
უცნობები და განტოლებები ბიშიფის გამარტივებული მეთოდისათვის
|
ამ მეთოდით ძალების ჰორიზონტალური წონასწორობა სრულად არ კმაყოფილდება, ამიტომ ამ მეთოდის გამოყენება ფსევდო-სტატიკური გაანგარიშებისათვის, სადაც დამატებითი ჰორიზონტალური ძალებია მოდებული, კითხვის ქვეშაა. თუ ნაგებობა დაპროექტებულია ამ მეთოდით, საბოლოო ანგარიში უნდა შემოწმდეს სპენსერის მეთოდით.
ნახ.8. ტიპური ბლოკი და ძალები ბიშოფის გამარტივებული მეთოდისათვის a) ფერდობი და ტიპური დაცურების ზედაპირი; b) ტიპური ბლოკი.
სპენსერის მეთოდი
[რედაქტირება]ამ მეთოდის მიხედვით ბლოკზე მოქმედი გვერდული ძალები პარალელურია. მაგალითად, ყველა გვერდული ძალა დახრილია ერთი და იგივე კუთხით. ნორმალური ძალა ბლოკის ძირზე მოქმედებს ძირის ცენტრში - ეს დაშვება მცირე გავლენას ახდენს საბოლოო ანგარიშზე. მეთოდი სრულად აკმაყოფილებს როგორც ძალის, ასევე მომენტის წონასწორობის მოთხოვნას. ამ მეთოდის გამოყენება სასურველია სტატიკური მდგრადობის სრული ანგარიშისათვის და როგორც მაკონტროლებელი ფერდობების მდგრადობის მარტივი მეთოდებით ანგარიშისას. ნახ.9-ზე მოცემულია ტიპური ბლოკთაშორისი საზღვარი AB, და ძალები, რომლებიც მოქმედებენ მასზე. მთლიანი ბლოკთაშორისი ძალა, Z, მოქმედებს θ კუთხით ჰორიზონტალურ ღერძთან და იგი არის ტოლქმედი შემდეგი 3 ძალისა: ნორმალური ეფექტური ძაბვით გამოწვეული პ’ძალის;ძვრის ძალის S/Fv = 1/Fv(c’H + p’tanφ’) = Zsin θ , სადაც Fv არის უსაფრ φ’არის ხახუნის კუთხე ეფექტურ ძაბვასთან მიმართებაში, c’არის შეჭიდულობა ეფექტურ ძაბვასთან მიმართებაში; და ფოროვანი წყლის დაწნევით გამოწვეული, W, ძალის. თუ დავუშვებთ ფოროვანი წყლის დაწნევის თანაბარ განაწილებას, მაშინ B-სთან ეს დაწნევა ტოლი იქნება B=ruγH-სა, სადაც γ არის ფუძის სიმკვრივე, H არის ბლოკთაშორისი საზღვრის, AB, სიმაღლე და ru არის ფოროვანი დაწნევის კოეფიციენტი. W=1/2ruH2 . /23/
უსაფრთხოების ფაქტორის განსაზღვრა ხდება შემდეგნაირად:
- Fv =1/zsinθ [c’H +tan φ’(zcosθ – 1/2 ruγH2)] (15)
უცნობები და განტოლებები, რომელიც გამოიყენება ამ მეთოდში, მოცემულია 7 ცხრილში.
ნახ.9. ბლოკთაშორის საზღვარზე მოქმედი ძალები სპენსერის მეთოდისათვის
ცხრილი 7
უცნობები და განტოლებები სპენსერის მეთოდისათვის
|
სპენსერის მეთოდი (1967) შეიძლება გამოყენებული იქნეს არაწრიული დაცურების ზედაპირისთვისაც. მეთოდი თხოულობს აუცილებლად კომპიუტერულ პროგრამას ანგარიშისათვის, რადგანაც მომენტისა და ძალის წონასწორობა უნდა დაკმაყოფილდეს ყოველი ბლოკისათვის და ანგარიში გრძელდება უსაფრთხოების ფაქტორის განსაზღვრის მცდელობათა გარკვეული რიცხვისათვის და ბლოკთაშორისი ძალების დახრის განსაზღვრისათვის.
ძალთა წონასწორობის მეთოდი მოდიფიცირებულ შვედურ მეთოდთან ერთად
[რედაქტირება]ამ მეთოდის მიხედვით კმაყოფილდება ძალთა წონასწორობა ორივე - ჰორიზონტალური და ვერტიკალური მიმართულებით, მაგრამ არ კმაყოფილდება მომენტთა წონასწორობის პირობა. ეს მეთოდი ეფუძნება ძალთა დახრის კუთხის, θ-ს, დაშვებას ბლოკებს შორის (ნახ.10) უცნობებისა და განტოლებების რიცხვი მოყვანილია 8 ცხრილში /3/:
ნახ.10-ზე მოცემული zi და zi+1 სიდიდეები წარმოადგენენ ძალებს ბლოკისათვის ფერდობის ზემოთ და ქვემოთ მიმართულებით. θ არის ბლოკთაშორისი ძალების დახრის კუთხე.
ნახ. 10. ტიპური ბლოკი და ძალები მოდიფიცირებული შვედური მეთოდისათვის ბლოკთაშორისი ძალების, θ, სავარაუდო მიმართულება.
ცხრილი 8.
უცნობები და განტოლებები ძალთა წონასწორობის მეთოდისათვის
|
ძალების გამოთვლა იწყება პირველი ბლოკიდან, სადაც zi=0 და პროცესი გრძელდება ყველა ბლოკისათვის ბოლო ბლოკის ჩათვლით. ანგარიში წარმოებს ფერდობის წვერიდან ძირისაკენ. ბლოკთაშორისი ძალის zi+1-ის მნიშვნელობა ფერდობის ბოლო ბლოკისათვის (დაცურების ზედაპირის ძირი) იქნება ნული, თუ უსაფრთხოების ფაქტორის მნიშვნელობა სწორად არის განსაზღვრული. თუ ეს ძალა არ არის ნულის ტოლი, მაშინ უნდა შეირჩეს უსაფრთხოების ფაქტორის ახალი სიდიდე და პროცესი განმეორდეს მანამ, ვიდრე ამ ძალის მნიშვნელობა 0-ს არ გაუტოლდება.
ამ მეთოდისათვის დამახასიათებელია ის, რომ ბლოკთაშორისი ძალების დახრის კუთხის მიმართ უსაფრთხოების ფაქტორი მგრძნობიარეა, მისი მნიშვნელობა შეიძლება მივიღოთ გადაჭარბებული ან შემცირებული მნიშვნელობით. ძალთა წონასწორობის მეთოდი ერთადერთია ზღვრული წონასწორობის მეთოდებს შორის, რომელიც შეიძლება გამოყენებული იქნეს არაწრიული დაცურების ზედაპირისათვის. ეს მეთოდი გაცილებით მარტივია სპენსერის მეთოდთან შედარებით, მაგრამ სიზუსტეში მას ჩამოუვარდება. ეს ორი მეთოდი იძლევა იდენტურ შედეგებს, თუ გამოყენებული იქნება გვერდული ძალების დახრის კუთხის ერთი და იგივე მნიშვნელობა.
ჯანბუს ბლოკების განზოგადოებული მეთოდი
[რედაქტირება]ამ მეთოდში /4/ დაშვებულია n რიცხვი ნორმალური ძალის, N, და (n-1) რიცხვი ბლოკთაშორისი ძალის, E-ს, მოდების წერტილისა. რადგანაც ამ შემთხვევაში 1 დაშვებით მეტია, ვიდრე საჭიროა, აქედან გამომდინარე, ტექნიკურად ზუსტი გადაწყვეტის მიღება არ ხდება. ამ მეთოდში ბოლო ძალის, N-ის, პოზიცია არ გამოიყენება და მომენტის წონასწორობა ბოლო ბლოკისათვის არ კმაყოფილდება.
მორგენშტერნისა და პრაისის მეთოდი
[რედაქტირება]ამ მეთოდში /4/ დაშვებულია n რიცხვი N ძალის მოდების წერტილისა და (n-1) რიცხვი ბლოკთაშორისი ჰორიზონტალური, E, და ვერტიკალური, X, ძალებს შორის ფარდობითი კავშირისა. როცა ანგარიშში უსასრულოდ მცირე ბლოკია გამოყენებული, ნ მიისწრაფის უსასრულობისაკენ, მაგრამ პრინციპები იგივე რჩება. რადგანაც კეთდება 1-ზე მეტი დაშვება, ვიდრე მოთხოვნილია, შემოყვანილია ზედმეტი უცნობი და ამიტომ სტატიკური წონასწორობა კმაყოფილდება ზუსტად.
სარმას მეთოდი
[რედაქტირება]განიხილება პოტენციალური დაცურების მასების წონასწორობა. დაცურების მასებიდაკავშირებულია ABCD დაცურების ხაზთან და იყოფა ნ ვერტიკალურ ბლოკად. ნახ.11-ზე მოცემულია I ბლოკი და მასზე მოქმედი ძალები. ნორმალური ძალა Ni ითვლება მოდებულად ბლოკის შუა წერტილში. უნდა გამოითვალოს კრიტიკული ჰორიზონტალური აჩქარება, რომელიც საჭიროა თავისუფალ ზედაპირთან დაკავშირებული ფუძის მასების ზღვრულ წონასწორობის მდგომარეობაში ყოფნისათვის. აქედან გამომდინარე ეს აჩქარება არის საზომი უსაფრთხოების ფაქტორისა /35/. ბლოკის ვერტიკალური და ჰორიზონტალური წონასწორობიდან მიღებულია შემდეგი გამოსახულებები:
- Ni cosαi + Ti sin αi = Wi - DXi (16)
- Ti cosαi - Ni sinαi = KWi + DEi (17)
იგულისხმება, რომ KWi ძალის მოქმედებით ზედაპირზე მობილიზებულია სრული ძვრის სიმტკიცე, რაც იმას ნიშნავს, რომ უსაფრთხოების ფაქტორი ტოლია 1-ს და აქედან გამომდინარე K წარმოადგენს კრიტიკულ აჩქარებას როგორც საკუთარი წონის აჩქარების ნაწილს. მთლიანი მასების სრული წონასწორობისათვის დაკმაყოფილებული უნდა იქნეს მომენტის წონასწორობის პირობა. სირთულე მდგომარეობს ბლოკთაშორისი ძალების Xi-ის განაწილების დადაგენაში. საპოვნელია X ძალების ის მნიშვნელობები, რომლებიც დააკმაყოფილებენ წონასწორობის განტოლებებს. ითვლება, რომ ცნობილია ამ ძალების განაწილების ფორმა და არა მათი სიდიდეები. უსაფრთხოების ფაქტორი, FLi, ბლოკის ვერტიკალურ ნაწილში (მაგ. უსაფრთხოების ლოკალური ფაქტორი) შეიძლება გამოითვალოს ასე:
- FLi = [(Ei – PWi) tan φi + ciHi] / Xi (18)
სადაც tan φi და ci არის i სექციის საშუალო ძვრის სიმტკიცის პარამეტრი.
უსაფრთხოების ფაქტორის სიდიდე, რომელიც იძლევა ნულოვან კრიტიკულ აჩქარებას, არის უსაფრთხოების ფაქტორი, რომელიც მიღებულია სეისმური ზემოქმედების გარეშე.
ნახ.11. ტიპური ბლოკი და მასზე მოქმედი ძალები სარმას მეთოდისათვის
წარწერები ნახაზზე:
- Ei და Ei+1 არის ჰორიზონტალური ძალვა i და i+1 ბლოკის ვერტიკალურ გვერდებზე, გამოხატული ეფექტურ ძალებში;
- Xi და Xi+1 არის ძვრის ძალა i და i+1 ბლოკის ვერტიკალურ გვერდებზე, შესაბამისად;
- Pwi და Pwi+1 არის ბლოკის ვერტიკალურ i და i+1 გვერდებზე მოქმედი წყლის დაწნევის ტოლქმედი, შესაბამისად;
- Wi არის ბლოკის წონა;
- Ni არის ბლოკ 1-ზე მოქმედი ბლოკის სიმძიმის ცენტრში მოდებული ჰორიზონტალური ძალა;
- ui არის ბლოკის ფუძეზე მოქმედი ნორმალური ძალა, გამოხატული ეფექტურ ძაბვებში;
- Ni არის ბლოკის ფუძეზე მოქმედი ფოროვანი დაწნევით გამოწვეული ძალა;
- Ti არის ბლოკის ძვრის ძალა;
- zi დაცურების ხაზის ზემოთ Ei ძალის მოდების წერტილის სიმაღლე;
- ci და φi არის ბლოკის ფუძის მასალის ეფექტური ძვრის სიმტკიცის პარამეტრები;
- Ni = N’i + ui,
- Ei = E’i + Pwi;
- Hi არის ი-ური ნაწილის დაცურების მასების სიმაღლე;
- Kc არის კრიტიკული ჰორიზონტალური აჩქარება, როგორც ნაწილი სიმძიმის ძალის აჩქარებისა, რომელიც საჭიროა :დაცურების ხაზის ზემოთ მდებარე მასების ზღვრული წონასწორობის მდგომარეობაში შესანარჩუნებლად;
- h არის ბლოკის სიგანე
- αi არის BC ხაზის მიერ შექმნილი კუთხე ჰორიზონტთან;
- xi და yi არის ბლოკის ძირის საშუალო წერტილის კოორდინატები ღერძების მიმართ;
- xg და yg არის დაცურებული მასების სიმძიმის ცერტრის კოორდინატები ღერძების მიმართ;
- DEi =Ei+1 -Ei;
- DXi = Xi+1 –Xi;
შენიშვნა: ზემოთ მოყვანილ მეთოდებში გათვალისწინებულია წონასწორობის ყველა პირობის დაკმაყოფილება წინასწარ მიღებული დაშვებებით. ბიშოფის მოდიფიცირებული მეთოდი, მართალია, არ აკმაყოფილებს წონასწორობის ყველა პირობას, მაგრამ საკმაოდ ზუსტია მხოლოდ დაცურების წრიული ზედაპირისათვის. ყველა დანარჩენი მეთოდებით შეიძლება განისაზღვროს ნებისმიერი დაცურების ზედაპირის უსაფრთხოების ფაქტორის სიდიდე, ოღონდ სირთულეები დაკავშირებულია შესაბამისი ძალების განაწილების შერჩევასთან მორგენშტერნისა და პრაისის და სარმას მეთოდებში, აგრეთვე რიცხვითი არასტაბილურობის ხშირ პრობლემასთან, რაც გვხვდება ჯანბუს განზოგადებულ მეთოდში. ამიტომ ამ მეთოდების გამოყენება მოუხერხებელია საინჟინრო პრაქტიკისათვის. ნებისმიერი მოხაზულობის დაცურების ზედაპირისათვის უმჯობესია გამოყენებული იქნეს სპენსერის მეთოდი, ხოლო ბიშოფის მოდიფიცირებული მეთოდი - წრიული დაცურების ზედაპირისათვის. თუ მდგრადობის ანგარიშები ჩატარებულია სხვა მეთოდებით, საჭიროა სტატიკური უსაფრთხოების ფაქტორი კრიტიკული დაცურების ზედაპირისათვის შემოწმდეს სპენსერის ან ბიშოფის მეთოდებით /33/.
სასრულო ელემენტის მეთოდი
[რედაქტირება]თუ საჭიროა სასრულო ელემენტის მეთოდით უსაფრთხოების ფაქტორის იმ სიდიდის განსაზღვრა, რომელიც ექვივალენტური იქნება ზღვრული წონასწორობის მეთოდით გამოთვლილისა, უნდა ჩატარდეს შემდეგი ოპერაციები: /3/
- სასრულო ელემენტის მეთოდით გაანგარიშებული უნდა იქნეს ძაბვები ფერდობისათვის;
- ამორჩეული უნდა იქნეს საცდელი დაცურების ზედაპირი;
- დაცურების ზედაპირი უნდა დაიყოს სეგმენტებად;
- გამოითვალოს ნორმალური და ძვრის ძაბვები შერჩეული დაცურების ზედაპირის გასწვრივ;
- გამოყენებული უნდა იყოს ნორმალური ძაბვებისა და ძვრისადმი სიმტკიცის პარამეტრები c’ და φ’, რათა განისაზღვროს საჭირო სიმტკიცე ძვრისადმი დაცურების ზედაპირის გასწვრივ წერტილებში;
- გამოითვალოს მთლიანი უსაფრთხოების ფაქტორი შემდეგნაირად:
- F = Σ siΔl /Στi Δl (15)
- სადაც si არის შესაბამისი ძვრისადმი სიმტკიცე;
- τi არის ძვრის ძაბვა;
- Δl არის სეგმენტებად დაყოფილი დაცურების ზედაპირის თითოეული სეგმენტის სიგრძე.
კვლევებმა აჩვენა, რომ უსაფრთხოების ფაქტორის მნიშვნელობა, რომელიც გამოითვლება ზემოთ მოყვანილი მიმდევრობით, იდენტურია იმ უსაფრთხოების ფაქტორის მნიშვნელობისა, რომელიც გამოითვალა ზღვრული წონასწორობის ზუსტი მეთოდებით.
ლოკალური უსაფრთხოების ფაქტორის გამოთვლა შესაძლებელია ძაბვებისა და ძვრის სიმტკიცის მნიშვნელობებით ფერდობის შერჩეულ წერტილში. ლოკალურად გამოთვლილი უსაფრთხოების ფაქტორის მნიშვნელობა შეიძლება უფრო დაბალი იყოს, ვიდრე (15) ტოლობიდან ან ზღვრული წონასწორობის მეთოდიდან გამოთვლილი მთლიანი მინიმალური უსაფრთხოების ფაქტორი. ლოკალური ფაქტორის მნიშვნელობა 1-ზე ნაკლები ჯერ კიდევ არ მიუთითებს ფერდობის არასტაბილურობაზე. ძაბვები გადანაწილებული იქნება დაზიანების ერთი წერტილიდან მეორე წერტილამდე, სადაც უსაფრთხოების ფაქტორი 1-ზე მეტი იქნება. ამ შემთხვევაში ფერდობი იქნება სტაბილური.